- Новости
-
Олимпиада
- Рекомендуемая литература
- Положение об олимпиаде
- Методическая программа
- Регламент олимпиады
- Критерии оценивания
- Места проведения олимпиады
- История олимпиады
- Текущая олимпиада
- 2023-2024 учебный год
- 2022-2023 учебный год
- 2021-2022 учебный год
- 2020-2021 учебный год
- 2019-2020 учебный год
- 2018-2019 учебный год
- 2017-2018 учебный год
- 2016-2017 учебный год
- 2015-2016 учебный год
- 2014-2015 учебный год
- 2013-2014 учебный год
- 2012-2013 учебный год
- 2011-2012 учебный год
- 2010-2011 учебный год
- 2009-2010 учебный год
- 2008-2009 учебный год
- 2007-2008 учебный год
- Прочее
- Астрономические кружки
- Летние школы
- Абитуриенту
- Форум
- Ссылки
Задачи и решения (11 класс)
1. Каков бы был период обращения Юпитера относительно Солнца, если бы масса Солнца была в 10 раз больше, чем на самом деле? Считать, что радиус орбиты Юпитера не меняется и равен 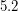 а.е.
Решение: Для решения этой задачи следует воспользоваться так называемым "обобщенным" III законом Кеплера:
а.е.
Решение: Для решения этой задачи следует воспользоваться так называемым "обобщенным" III законом Кеплера:
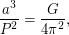 где
где 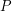 - период обращения планеты,
- период обращения планеты,  - радиус (а точнее, большая полуось) ее орбиты,
- радиус (а точнее, большая полуось) ее орбиты,  - масса Солнца,
- масса Солнца, 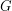 - гравитационная постоянная.
Отсюда получаем
- гравитационная постоянная.
Отсюда получаем
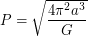 откуда следует, что при неизменном радиусе орбиты
откуда следует, что при неизменном радиусе орбиты 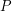 обратно пропорционален
обратно пропорционален 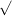 . Таким образом искомый период был бы в
. Таким образом искомый период был бы в 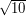 раз меньше, чем на самом деле.
Настоящий период обращения Юпитера можно определить из "простого" III закона Кеплера, сравнив орбиту Юпитера с орбитой Земли:
раз меньше, чем на самом деле.
Настоящий период обращения Юпитера можно определить из "простого" III закона Кеплера, сравнив орбиту Юпитера с орбитой Земли:
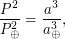 где
где 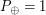 год - период обращения Земли, а
год - период обращения Земли, а 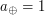 а.е. - радиус ее орбиты. Отсюда
а.е. - радиус ее орбиты. Отсюда 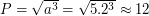 лет. Получаем, что искомый период был бы равен
лет. Получаем, что искомый период был бы равен 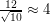 года.
2. Могут ли какие-либо галилеевы спутники Юпитера при наблюдении с Юпитера находиться в "полнолунии"? Радиусы орбит спутников (в радиусах Юпитера) составляют: Ио -
года.
2. Могут ли какие-либо галилеевы спутники Юпитера при наблюдении с Юпитера находиться в "полнолунии"? Радиусы орбит спутников (в радиусах Юпитера) составляют: Ио - 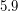 , Европа -
, Европа - 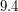 , Ганимед -
, Ганимед - 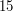 , Каллисто -
, Каллисто - 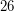 .
Решение: Вспомним, что наклон орбит галилеевых спутников Юпитера к плоскости эклиптики практически нулевой. Тогда вопрос состоит в том, попадут ли спутники при приближении к фазе "полнолуния" в тень Юпитера или нет. Очевидно, что шансы не попасть в тень выше всего у наиболее далекого спутника - Каллисто. Угловой диаметр Юпитера при наблюдении с Каллисто можно легко оценить, он составит
.
Решение: Вспомним, что наклон орбит галилеевых спутников Юпитера к плоскости эклиптики практически нулевой. Тогда вопрос состоит в том, попадут ли спутники при приближении к фазе "полнолуния" в тень Юпитера или нет. Очевидно, что шансы не попасть в тень выше всего у наиболее далекого спутника - Каллисто. Угловой диаметр Юпитера при наблюдении с Каллисто можно легко оценить, он составит 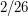 радиана, т.е. примерно
радиана, т.е. примерно 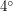 . Так как угловой размер диска Солнца при наблюдении с орбиты Юпитера намного меньше - около
. Так как угловой размер диска Солнца при наблюдении с орбиты Юпитера намного меньше - около 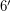 (можно вспомнить, что угловой размер диска Солнца при наблюдении с Земли примерно равен
(можно вспомнить, что угловой размер диска Солнца при наблюдении с Земли примерно равен 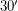 , а Юпитер находится в 5 раз дальше от Солнца, чем Земля), то это означает, что даже Каллисто (а, следовательно, и все остальные галилеевы спутники тоже) окажутся глубоко в тени Юпитера.
3. Почему в веществе самых старых звезд Галактики очень мало тяжелых элементов, а в веществе самых молодых, наоборот, их содержание относительно велико?
Решение: Самые старые звезды образовались из бедного тяжелыми элементами протогалактического газового облака. Массивные звезды, быстро эволюционируя, взрывались и обогащали межзвездную среду образовавшимися в них тяжелыми элементами. Следующие поколения звезд образовывались из вещества с большим содержанием тяжелых элементов.
4. Может ли искусственный спутник иметь такую орбиту, чтобы его трасса проходила бы только над следующими частями света:
a) над Европой?
b) над Африкой?
c) и над Европой, и над Африкой?
Решение: Проще всего ответить на вопрос b) - так как через Африку проходит экватор, то геостационарный спутник будет искомым.
Подходящими для двух остальных вопросов спутниками могут быть только суточные спутники (с периодом обращения, равным суткам), в противном случае орбита спутника будет перемещаться по долготе из-за вращения Земли, и такой спутник рано или поздно пролетит, например, над Америкой. Орбита суточного спутника с некоторым наклоном, меньшим
, а Юпитер находится в 5 раз дальше от Солнца, чем Земля), то это означает, что даже Каллисто (а, следовательно, и все остальные галилеевы спутники тоже) окажутся глубоко в тени Юпитера.
3. Почему в веществе самых старых звезд Галактики очень мало тяжелых элементов, а в веществе самых молодых, наоборот, их содержание относительно велико?
Решение: Самые старые звезды образовались из бедного тяжелыми элементами протогалактического газового облака. Массивные звезды, быстро эволюционируя, взрывались и обогащали межзвездную среду образовавшимися в них тяжелыми элементами. Следующие поколения звезд образовывались из вещества с большим содержанием тяжелых элементов.
4. Может ли искусственный спутник иметь такую орбиту, чтобы его трасса проходила бы только над следующими частями света:
a) над Европой?
b) над Африкой?
c) и над Европой, и над Африкой?
Решение: Проще всего ответить на вопрос b) - так как через Африку проходит экватор, то геостационарный спутник будет искомым.
Подходящими для двух остальных вопросов спутниками могут быть только суточные спутники (с периодом обращения, равным суткам), в противном случае орбита спутника будет перемещаться по долготе из-за вращения Земли, и такой спутник рано или поздно пролетит, например, над Америкой. Орбита суточного спутника с некоторым наклоном, меньшим 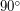 , будет представлять собой "восьмерку" с центром на экваторе, крайние точки которой будут иметь широту, равную наклону орбиты. Можно подобрать наклон таким образом, чтобы спутник пролетал над Европой (при этом наклон должен быть больше
, будет представлять собой "восьмерку" с центром на экваторе, крайние точки которой будут иметь широту, равную наклону орбиты. Можно подобрать наклон таким образом, чтобы спутник пролетал над Европой (при этом наклон должен быть больше 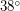 - это широта самой южной точки Европы) и не пролетал над Антарктидой (наклон должен быть меньше
- это широта самой южной точки Европы) и не пролетал над Антарктидой (наклон должен быть меньше 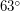 - широты самой северной точки Антарктиды). Реально нижняя граница наклона больше - при малом наклоне одна из петель "восьмерки" может зацепить Азию.
Однако при этом не удастся сделать так, чтобы спутник не пролетал над Африкой, поэтому ответ на вопрос c) - может, это должен быть суточный спутник с наклоном около
- широты самой северной точки Антарктиды). Реально нижняя граница наклона больше - при малом наклоне одна из петель "восьмерки" может зацепить Азию.
Однако при этом не удастся сделать так, чтобы спутник не пролетал над Африкой, поэтому ответ на вопрос c) - может, это должен быть суточный спутник с наклоном около 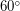 ; ответ на вопрос a) - не может.
Примечание: естественно, в решении не требовалось указывать предельные значения наклонов орбит спутников.
5. Десять солнцеподобных звезд свалили в кучу и сделали одну белую звезду главной последовательности. Как изменилась светимость такой звезды, если ее средняя плотность в три раза меньше солнечной?
Решение: Светимость звезды (
; ответ на вопрос a) - не может.
Примечание: естественно, в решении не требовалось указывать предельные значения наклонов орбит спутников.
5. Десять солнцеподобных звезд свалили в кучу и сделали одну белую звезду главной последовательности. Как изменилась светимость такой звезды, если ее средняя плотность в три раза меньше солнечной?
Решение: Светимость звезды (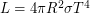 ) определяется температурой и площадью поверхности звезды. Звезда белая, т.е. ее температура около
) определяется температурой и площадью поверхности звезды. Звезда белая, т.е. ее температура около 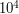 К. Она в
К. Она в 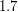 раза больше температуры Солнца (
раза больше температуры Солнца (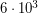 К), и за счет изменения температуры светимость увеличилась в
К), и за счет изменения температуры светимость увеличилась в 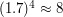 раз.
Так как масса звезды стала в 10 раз больше, а плотность в 3 раза меньше, то объем звезды увеличился в 30 раз. Поскольку объем пропорционален кубу радиуса, то радиус новой звезды в
раз.
Так как масса звезды стала в 10 раз больше, а плотность в 3 раза меньше, то объем звезды увеличился в 30 раз. Поскольку объем пропорционален кубу радиуса, то радиус новой звезды в ![$ \sqrt[3]{30} $](/files/tex/d7cf8e7f828d23402232e8d7302579122fd91589.png) раз больше старого радиуса, а площадь поверхности, следовательно, в
раз больше старого радиуса, а площадь поверхности, следовательно, в 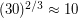 раз больше прежней. Таким образом, суммарная светимость новой звезды возросла в
раз больше прежней. Таким образом, суммарная светимость новой звезды возросла в 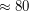 раз.
раз.
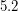 а.е.
Решение: Для решения этой задачи следует воспользоваться так называемым "обобщенным" III законом Кеплера:
а.е.
Решение: Для решения этой задачи следует воспользоваться так называемым "обобщенным" III законом Кеплера:
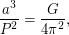 где
где 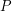 - период обращения планеты,
- период обращения планеты,  - радиус (а точнее, большая полуось) ее орбиты,
- радиус (а точнее, большая полуось) ее орбиты,  - масса Солнца,
- масса Солнца, 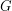 - гравитационная постоянная.
Отсюда получаем
- гравитационная постоянная.
Отсюда получаем
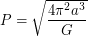 откуда следует, что при неизменном радиусе орбиты
откуда следует, что при неизменном радиусе орбиты 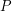 обратно пропорционален
обратно пропорционален 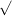 . Таким образом искомый период был бы в
. Таким образом искомый период был бы в 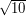 раз меньше, чем на самом деле.
Настоящий период обращения Юпитера можно определить из "простого" III закона Кеплера, сравнив орбиту Юпитера с орбитой Земли:
раз меньше, чем на самом деле.
Настоящий период обращения Юпитера можно определить из "простого" III закона Кеплера, сравнив орбиту Юпитера с орбитой Земли:
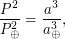 где
где 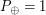 год - период обращения Земли, а
год - период обращения Земли, а 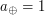 а.е. - радиус ее орбиты. Отсюда
а.е. - радиус ее орбиты. Отсюда 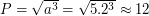 лет. Получаем, что искомый период был бы равен
лет. Получаем, что искомый период был бы равен 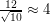 года.
2. Могут ли какие-либо галилеевы спутники Юпитера при наблюдении с Юпитера находиться в "полнолунии"? Радиусы орбит спутников (в радиусах Юпитера) составляют: Ио -
года.
2. Могут ли какие-либо галилеевы спутники Юпитера при наблюдении с Юпитера находиться в "полнолунии"? Радиусы орбит спутников (в радиусах Юпитера) составляют: Ио - 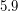 , Европа -
, Европа - 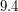 , Ганимед -
, Ганимед - 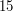 , Каллисто -
, Каллисто - 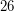 .
Решение: Вспомним, что наклон орбит галилеевых спутников Юпитера к плоскости эклиптики практически нулевой. Тогда вопрос состоит в том, попадут ли спутники при приближении к фазе "полнолуния" в тень Юпитера или нет. Очевидно, что шансы не попасть в тень выше всего у наиболее далекого спутника - Каллисто. Угловой диаметр Юпитера при наблюдении с Каллисто можно легко оценить, он составит
.
Решение: Вспомним, что наклон орбит галилеевых спутников Юпитера к плоскости эклиптики практически нулевой. Тогда вопрос состоит в том, попадут ли спутники при приближении к фазе "полнолуния" в тень Юпитера или нет. Очевидно, что шансы не попасть в тень выше всего у наиболее далекого спутника - Каллисто. Угловой диаметр Юпитера при наблюдении с Каллисто можно легко оценить, он составит 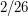 радиана, т.е. примерно
радиана, т.е. примерно 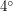 . Так как угловой размер диска Солнца при наблюдении с орбиты Юпитера намного меньше - около
. Так как угловой размер диска Солнца при наблюдении с орбиты Юпитера намного меньше - около 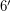 (можно вспомнить, что угловой размер диска Солнца при наблюдении с Земли примерно равен
(можно вспомнить, что угловой размер диска Солнца при наблюдении с Земли примерно равен 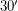 , а Юпитер находится в 5 раз дальше от Солнца, чем Земля), то это означает, что даже Каллисто (а, следовательно, и все остальные галилеевы спутники тоже) окажутся глубоко в тени Юпитера.
3. Почему в веществе самых старых звезд Галактики очень мало тяжелых элементов, а в веществе самых молодых, наоборот, их содержание относительно велико?
Решение: Самые старые звезды образовались из бедного тяжелыми элементами протогалактического газового облака. Массивные звезды, быстро эволюционируя, взрывались и обогащали межзвездную среду образовавшимися в них тяжелыми элементами. Следующие поколения звезд образовывались из вещества с большим содержанием тяжелых элементов.
4. Может ли искусственный спутник иметь такую орбиту, чтобы его трасса проходила бы только над следующими частями света:
a) над Европой?
b) над Африкой?
c) и над Европой, и над Африкой?
Решение: Проще всего ответить на вопрос b) - так как через Африку проходит экватор, то геостационарный спутник будет искомым.
Подходящими для двух остальных вопросов спутниками могут быть только суточные спутники (с периодом обращения, равным суткам), в противном случае орбита спутника будет перемещаться по долготе из-за вращения Земли, и такой спутник рано или поздно пролетит, например, над Америкой. Орбита суточного спутника с некоторым наклоном, меньшим
, а Юпитер находится в 5 раз дальше от Солнца, чем Земля), то это означает, что даже Каллисто (а, следовательно, и все остальные галилеевы спутники тоже) окажутся глубоко в тени Юпитера.
3. Почему в веществе самых старых звезд Галактики очень мало тяжелых элементов, а в веществе самых молодых, наоборот, их содержание относительно велико?
Решение: Самые старые звезды образовались из бедного тяжелыми элементами протогалактического газового облака. Массивные звезды, быстро эволюционируя, взрывались и обогащали межзвездную среду образовавшимися в них тяжелыми элементами. Следующие поколения звезд образовывались из вещества с большим содержанием тяжелых элементов.
4. Может ли искусственный спутник иметь такую орбиту, чтобы его трасса проходила бы только над следующими частями света:
a) над Европой?
b) над Африкой?
c) и над Европой, и над Африкой?
Решение: Проще всего ответить на вопрос b) - так как через Африку проходит экватор, то геостационарный спутник будет искомым.
Подходящими для двух остальных вопросов спутниками могут быть только суточные спутники (с периодом обращения, равным суткам), в противном случае орбита спутника будет перемещаться по долготе из-за вращения Земли, и такой спутник рано или поздно пролетит, например, над Америкой. Орбита суточного спутника с некоторым наклоном, меньшим 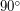 , будет представлять собой "восьмерку" с центром на экваторе, крайние точки которой будут иметь широту, равную наклону орбиты. Можно подобрать наклон таким образом, чтобы спутник пролетал над Европой (при этом наклон должен быть больше
, будет представлять собой "восьмерку" с центром на экваторе, крайние точки которой будут иметь широту, равную наклону орбиты. Можно подобрать наклон таким образом, чтобы спутник пролетал над Европой (при этом наклон должен быть больше 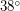 - это широта самой южной точки Европы) и не пролетал над Антарктидой (наклон должен быть меньше
- это широта самой южной точки Европы) и не пролетал над Антарктидой (наклон должен быть меньше 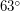 - широты самой северной точки Антарктиды). Реально нижняя граница наклона больше - при малом наклоне одна из петель "восьмерки" может зацепить Азию.
Однако при этом не удастся сделать так, чтобы спутник не пролетал над Африкой, поэтому ответ на вопрос c) - может, это должен быть суточный спутник с наклоном около
- широты самой северной точки Антарктиды). Реально нижняя граница наклона больше - при малом наклоне одна из петель "восьмерки" может зацепить Азию.
Однако при этом не удастся сделать так, чтобы спутник не пролетал над Африкой, поэтому ответ на вопрос c) - может, это должен быть суточный спутник с наклоном около 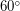 ; ответ на вопрос a) - не может.
Примечание: естественно, в решении не требовалось указывать предельные значения наклонов орбит спутников.
5. Десять солнцеподобных звезд свалили в кучу и сделали одну белую звезду главной последовательности. Как изменилась светимость такой звезды, если ее средняя плотность в три раза меньше солнечной?
Решение: Светимость звезды (
; ответ на вопрос a) - не может.
Примечание: естественно, в решении не требовалось указывать предельные значения наклонов орбит спутников.
5. Десять солнцеподобных звезд свалили в кучу и сделали одну белую звезду главной последовательности. Как изменилась светимость такой звезды, если ее средняя плотность в три раза меньше солнечной?
Решение: Светимость звезды (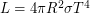 ) определяется температурой и площадью поверхности звезды. Звезда белая, т.е. ее температура около
) определяется температурой и площадью поверхности звезды. Звезда белая, т.е. ее температура около 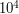 К. Она в
К. Она в 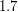 раза больше температуры Солнца (
раза больше температуры Солнца (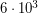 К), и за счет изменения температуры светимость увеличилась в
К), и за счет изменения температуры светимость увеличилась в 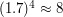 раз.
Так как масса звезды стала в 10 раз больше, а плотность в 3 раза меньше, то объем звезды увеличился в 30 раз. Поскольку объем пропорционален кубу радиуса, то радиус новой звезды в
раз.
Так как масса звезды стала в 10 раз больше, а плотность в 3 раза меньше, то объем звезды увеличился в 30 раз. Поскольку объем пропорционален кубу радиуса, то радиус новой звезды в ![$ \sqrt[3]{30} $](/files/tex/d7cf8e7f828d23402232e8d7302579122fd91589.png) раз больше старого радиуса, а площадь поверхности, следовательно, в
раз больше старого радиуса, а площадь поверхности, следовательно, в 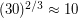 раз больше прежней. Таким образом, суммарная светимость новой звезды возросла в
раз больше прежней. Таким образом, суммарная светимость новой звезды возросла в 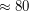 раз.
раз.
- Войдите или зарегистрируйтесь, чтобы получить возможность отправлять комментарии
2 задача
"Очевидно, что шансы не попасть в тень выше всего у наиболее далекого спутника - Каллисто."
Дайте пожалуйста пояснения этого факта...
Тень планеты
Тень планеты представляет собой конус, основание которого - сечение планеты, центр которого совпадает с центром планеты, и перпендикулярное плоскости орбиты планеты. Чем дальше спутник от планеты, тем в более узкую область тени планеты он попадает. Если спутник очень далеко, то у него есть шанс совсем не попасть в тень. Так что проверку в данной задаче целесоообразно начинать с самого далекого спутника. Совет: посмотрите в решениях 5-6 классов рисунок с лунным затмением, обратите внимание на форму тени и представьте спутник на разных расстояниях от планеты.