- Новости
-
Олимпиада
- Рекомендуемая литература
- Положение об олимпиаде
- Методическая программа
- Регламент олимпиады
- Критерии оценивания
- Места проведения олимпиады
- История олимпиады
- Текущая олимпиада
- 2023-2024 учебный год
- 2022-2023 учебный год
- 2021-2022 учебный год
- 2020-2021 учебный год
- 2019-2020 учебный год
- 2018-2019 учебный год
- 2017-2018 учебный год
- 2016-2017 учебный год
- 2015-2016 учебный год
- 2014-2015 учебный год
- 2013-2014 учебный год
- 2012-2013 учебный год
- 2011-2012 учебный год
- 2010-2011 учебный год
- 2009-2010 учебный год
- 2008-2009 учебный год
- 2007-2008 учебный год
- Прочее
- Астрономические кружки
- Летние школы
- Абитуриенту
- Форум
- Ссылки
Задачи и решения (10 класс)
- Учебный солнечный радиотелескоп Астрономического отделения СПбГУ представляет собой рефлектор со сферическим зеркалом, радиус кривизны которого равен 4 м. 14 сентября во время наблюдений телескоп был наведен на Солнце. Студент, проводивший наблюдения, выключил часовой механизм телескопа и отправился обедать. При возвращении с обеда он заметил, что тень от приемника излучения, находящегося в фокусе зеркала, оказалась на расстоянии
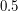 м от центра зеркала. Оцените время, которое студент потратил на обед.
м от центра зеркала. Оцените время, которое студент потратил на обед.
Решение: Как известно, фокусное расстояние сферического зеркала равно половине его радиуса кривизны. Таким образом, за время обеда Солнце прошло по небу угол в радианах, равный отношению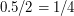 (тем, что тень двигалась по окружности с радиусом 4 м и, следовательно, рассматриваемый угол не является центральным для окружности, для оценки можно пренебречь).
(тем, что тень двигалась по окружности с радиусом 4 м и, следовательно, рассматриваемый угол не является центральным для окружности, для оценки можно пренебречь). 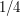 радиана - это чуть меньше
радиана - это чуть меньше 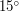 . Так как, по условию задачи, дело происходит 14 сентября, Солнце можно считать движущимся практически по небесному экватору (т.е. по дуге большого круга на небесной сфере), и тогда изменение положения Солнца на
. Так как, по условию задачи, дело происходит 14 сентября, Солнце можно считать движущимся практически по небесному экватору (т.е. по дуге большого круга на небесной сфере), и тогда изменение положения Солнца на 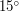 соответствует интервалу времени в 1 час (
соответствует интервалу времени в 1 час (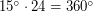 ). Отсюда получаем, что студент потратил на обед несколько менее 1 часа.
). Отсюда получаем, что студент потратил на обед несколько менее 1 часа. - 11 февраля 2009 года на высоте 800~км над поверхностью Земли столкнулись два спутника: "Космос-2251" и "Iridium 33". В момент столкновения угол между траекториями спутников составлял
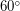 . Найдите диапазон возможных значений относительной скорости спутников при столкновении.
. Найдите диапазон возможных значений относительной скорости спутников при столкновении.
Решение: Спутники столкнулись на сравнительно небольшой высоте. С достаточной точностью можно считать, что в момент столкновения оба спутника находились в перигее (минимально возможная высота полета спутников составляет примерно 300 км, и относительная разница между расстоянием до центра Земли 7200 км и 6700 км невелика). Первая и вторая космические скорости на такой высоте также мало отличаются от <<наземных>> (они пропорциональны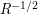 , поэтому отличие не превосходит 6%). Следовательно, минимально возможная скорость каждого спутника около 8 км/с, а максимально возможная - около 11 км/с. Если бы скорости спутников были одинаковыми и равнялись
, поэтому отличие не превосходит 6%). Следовательно, минимально возможная скорость каждого спутника около 8 км/с, а максимально возможная - около 11 км/с. Если бы скорости спутников были одинаковыми и равнялись  , то, так как угол между траекториями составлял
, то, так как угол между траекториями составлял 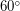 , относительная скорость сближения спутников также равнялась
, относительная скорость сближения спутников также равнялась  . Отсюда очевидно, что возможная относительная скорость спутников заключена в пределах от 8 км/с до 11 км/с.
. Отсюда очевидно, что возможная относительная скорость спутников заключена в пределах от 8 км/с до 11 км/с. - Параметры орбиты Венеры: большая полуось
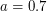 а.е., эксцентриситет
а.е., эксцентриситет 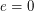 , наклон к плоскости эклиптики
, наклон к плоскости эклиптики 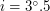 . Найдите максимально возможную высоту Венеры над горизонтом при наблюдении из Петербурга.
. Найдите максимально возможную высоту Венеры над горизонтом при наблюдении из Петербурга.
Решение: Так как широта Петербурга составляет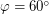 , а угол между экватором и эклиптикой
, а угол между экватором и эклиптикой 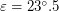 , то максимальная высота подъема Солнца над горизонтом в Петербурге равна
, то максимальная высота подъема Солнца над горизонтом в Петербурге равна 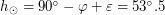 . Осталось вычислить, на какое максимальное расстояние от эклиптики Венера может отойти для земного наблюдателя. Рассмотрим треугольник
. Осталось вычислить, на какое максимальное расстояние от эклиптики Венера может отойти для земного наблюдателя. Рассмотрим треугольник 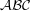 "Солнце-Земля-Венера" (соответственно). Очевидно, что угол при вершине, в которой находится Земля, будет максимальным в тот момент, когда Венера находится в нижнем соединении (т.е. расположена практически между Солнцем и Землей). Тогда сторона треугольника
"Солнце-Земля-Венера" (соответственно). Очевидно, что угол при вершине, в которой находится Земля, будет максимальным в тот момент, когда Венера находится в нижнем соединении (т.е. расположена практически между Солнцем и Землей). Тогда сторона треугольника 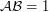 а.е.,
а.е., 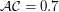 а.е.,
а.е., 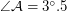 , а нам надо найти
, а нам надо найти 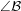 . Ввиду малости углов
. Ввиду малости углов 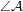 и
и 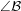 достаточно очевидно, что сторона треугольника
достаточно очевидно, что сторона треугольника 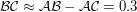 а.е. В принципе, для ее вычисления можно воспользоваться теоремой косинусов, но результат окажется таким же. Тогда мы можем записать теорему синусов для треугольника в виде:
а.е. В принципе, для ее вычисления можно воспользоваться теоремой косинусов, но результат окажется таким же. Тогда мы можем записать теорему синусов для треугольника в виде: 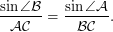 Синусы малых углов примерно равны самим углам, выраженным в радианах, но так как при переводе из градусов в радианы в равенстве слева и справа появятся одинаковые множители
Синусы малых углов примерно равны самим углам, выраженным в радианах, но так как при переводе из градусов в радианы в равенстве слева и справа появятся одинаковые множители 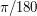 , то угол
, то угол 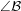 вычисляется как
вычисляется как 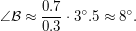 Таким образом, Венера для земного наблюдателя может подняться на
Таким образом, Венера для земного наблюдателя может подняться на 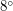 над эклиптикой и, следовательно, максимальная высота ее подъема над горизонтом в Петербурге составит
над эклиптикой и, следовательно, максимальная высота ее подъема над горизонтом в Петербурге составит 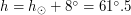 .
. - Предположим, что из фотосферы Солнца был взят кусочек вещества объемом в 1 л. Опасно ли будет для человека находиться на расстоянии в 1 м от этого кусочка? Характерная плотность вещества фотосферы -
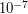 г/см
г/см .
.
Решение: Первое естественное желание, возникающее при решении задачи - сосчитать мощность излучения такого кусочка. Это достаточно легко сделать, воспользовавшись законом Стефана-Больцмана и зная, что температура фотосферы Солнца примерно равна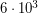 К. В результате окажется, что мощность равна
К. В результате окажется, что мощность равна 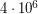 Вт, и кажется, что это очень опасно. Однако мощность излучения - не самая подходящая в данном случае характеристика. Дело в том, что кусочек очень быстро теряет энергию на излучение, поэтому светиться он будет очень непродолжительное время. Поэтому разумнее оценить внутреннюю энергию вещества светящегося кусочка, которую он может высветить. Энергия одного атома (а вещество фотосферы состоит в основном из атомов водорода) будет равна
Вт, и кажется, что это очень опасно. Однако мощность излучения - не самая подходящая в данном случае характеристика. Дело в том, что кусочек очень быстро теряет энергию на излучение, поэтому светиться он будет очень непродолжительное время. Поэтому разумнее оценить внутреннюю энергию вещества светящегося кусочка, которую он может высветить. Энергия одного атома (а вещество фотосферы состоит в основном из атомов водорода) будет равна 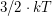 , где
, где 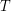 - температура,
- температура, 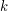 - постоянная Больцмана. Количество атомов, содержащихся в кусочке, равно
- постоянная Больцмана. Количество атомов, содержащихся в кусочке, равно 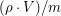 , где
, где 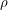 - плотность вещества,
- плотность вещества, 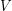 - его объем,
- его объем, 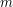 - масса одного атома. Тогда общая внутренняя энергия кусочка равна
- масса одного атома. Тогда общая внутренняя энергия кусочка равна 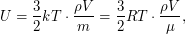 где
где 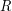 - универсальная газовая постоянная,
- универсальная газовая постоянная, 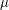 - молярная масса вещества (равная в нашем случае 1 г/моль). Подставив числовые данные, получаем, что внутренняя энергия кусочка равна примерно 7 Дж, что, очевидно, совершенно безвредно для человека.
- молярная масса вещества (равная в нашем случае 1 г/моль). Подставив числовые данные, получаем, что внутренняя энергия кусочка равна примерно 7 Дж, что, очевидно, совершенно безвредно для человека. - Ученые ведут наблюдения 20000 звезд по программе поиска внесолнечных планетных систем методом измерения лучевых скоростей. Известно, что у половины из этих звезд такие системы существуют. Известно также, что все планеты вызывают изменение скоростей звезд с амплитудой 20 м/с. Сколько существующих у этих звезд планетных систем астрономы обнаружить не смогут, если точность измерения лучевых скоростей составляет 2 м/с?
Решение: Орбита планеты вокруг звезды может быть ориентирована произвольным образом. В частности, в том случае, если плоскость орбиты перпендикулярна лучу зрения, изменение лучевой скорости звезды наблюдаться не будет. Требуется оценить относительную долю планетных орбит, которые будут почти перпендикулярны к лучу зрения - настолько, что изменение лучевой скорости окажется меньше 2 м/с. Представим себе сферу единичного радиуса, в которой случайным образом проведены различные диаметры (изображающие оси орбит рассматриваемых планет). Нас интересует относительная доля диаметров, концы которых попадают в два круга около выделенного диаметра (соответствующего направлению на Землю) - планетные системы, соответствующие этим диаметрам, наблюдаться не будут. Угол между каждым таким диаметром и выделенным диаметром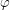 должен быть таким, чтобы выполнялось условие
должен быть таким, чтобы выполнялось условие 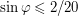 (так как синус угла - это коэффициент для вычисления проекции линейной скорости планеты на луч зрения). Отсюда получаем условие на сам угол:
(так как синус угла - это коэффициент для вычисления проекции линейной скорости планеты на луч зрения). Отсюда получаем условие на сам угол: 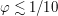 радиан. Два получившихся круга можно приближенно считать плоскими. Их радиусы равны
радиан. Два получившихся круга можно приближенно считать плоскими. Их радиусы равны 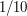 (мы рассматриваем сферу единичного радиуса), следовательно, суммарная площадь равна
(мы рассматриваем сферу единичного радиуса), следовательно, суммарная площадь равна 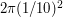 . Отношение этой площади к площади всей сферы даст нам долю планетных систем, которые не удастся наблюдать. Получаем, что доля таких систем равна
. Отношение этой площади к площади всей сферы даст нам долю планетных систем, которые не удастся наблюдать. Получаем, что доля таких систем равна 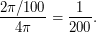 Так как планетные системы присутствуют только у половины наблюдаемых звезд, то таких звезд
Так как планетные системы присутствуют только у половины наблюдаемых звезд, то таких звезд 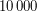 . Еще
. Еще 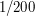 часть планетных систем нельзя обнаружить данным методом, таких звезд будет около 50.
часть планетных систем нельзя обнаружить данным методом, таких звезд будет около 50.
Комментарии
7 недель 2 дня назад
7 недель 2 дня назад
8 недель 4 дня назад
11 недель 17 часов назад
11 недель 1 день назад
14 недель 1 день назад
14 недель 1 день назад
19 недель 3 дня назад
19 недель 3 дня назад
22 недели 6 дней назад