- Новости
-
Олимпиада
- Рекомендуемая литература
- Положение об олимпиаде
- Методическая программа
- Регламент олимпиады
- Критерии оценивания
- Места проведения олимпиады
- История олимпиады
- Текущая олимпиада
- 2023-2024 учебный год
- 2022-2023 учебный год
- 2021-2022 учебный год
- 2020-2021 учебный год
- 2019-2020 учебный год
- 2018-2019 учебный год
- 2017-2018 учебный год
- 2016-2017 учебный год
- 2015-2016 учебный год
- 2014-2015 учебный год
- 2013-2014 учебный год
- 2012-2013 учебный год
- 2011-2012 учебный год
- 2010-2011 учебный год
- 2009-2010 учебный год
- 2008-2009 учебный год
- 2007-2008 учебный год
- Прочее
- Астрономические кружки
- Летние школы
- Абитуриенту
- Форум
- Ссылки
Задачи и решения (11 класс)
- Параметры орбиты Венеры: большая полуось
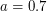 а.е., эксцентриситет
а.е., эксцентриситет 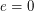 , наклон к плоскости эклиптики
, наклон к плоскости эклиптики 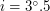 . Найдите максимально возможную высоту Венеры над горизонтом при наблюдении из Петербурга.
. Найдите максимально возможную высоту Венеры над горизонтом при наблюдении из Петербурга.
Решение: Так как широта Петербурга составляет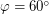 , а угол между экватором и эклиптикой
, а угол между экватором и эклиптикой 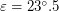 , то максимальная высота подъема Солнца над горизонтом в Петербурге равна
, то максимальная высота подъема Солнца над горизонтом в Петербурге равна 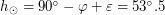 . Осталось вычислить, на какое максимальное расстояние от эклиптики Венера может отойти для земного наблюдателя. Рассмотрим треугольник
. Осталось вычислить, на какое максимальное расстояние от эклиптики Венера может отойти для земного наблюдателя. Рассмотрим треугольник 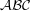 "Солнце-Земля-Венера" (соответственно). Очевидно, что угол при вершине, в которой находится Земля, будет максимальным в тот момент, когда Венера находится в нижнем соединении (т.е. расположена практически между Солнцем и Землей). Тогда сторона треугольника
"Солнце-Земля-Венера" (соответственно). Очевидно, что угол при вершине, в которой находится Земля, будет максимальным в тот момент, когда Венера находится в нижнем соединении (т.е. расположена практически между Солнцем и Землей). Тогда сторона треугольника 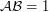 а.е.,
а.е., 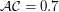 а.е.,
а.е., 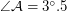 , а нам надо найти
, а нам надо найти 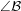 . Ввиду малости углов
. Ввиду малости углов 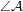 и
и 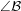 достаточно очевидно, что сторона треугольника
достаточно очевидно, что сторона треугольника 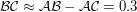 а.е. В принципе, для ее вычисления можно воспользоваться теоремой косинусов, но результат окажется таким же. Тогда мы можем записать теорему синусов для треугольника в виде:
а.е. В принципе, для ее вычисления можно воспользоваться теоремой косинусов, но результат окажется таким же. Тогда мы можем записать теорему синусов для треугольника в виде: 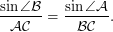 Синусы малых углов примерно равны самим углам, выраженным в радианах, но так как при переводе из градусов в радианы в равенстве слева и справа появятся одинаковые множители
Синусы малых углов примерно равны самим углам, выраженным в радианах, но так как при переводе из градусов в радианы в равенстве слева и справа появятся одинаковые множители 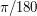 , то угол
, то угол 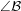 вычисляется как
вычисляется как 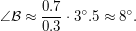 Таким образом, Венера для земного наблюдателя может подняться на
Таким образом, Венера для земного наблюдателя может подняться на 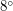 над эклиптикой и, следовательно, максимальная высота ее подъема над горизонтом в Петербурге составит
над эклиптикой и, следовательно, максимальная высота ее подъема над горизонтом в Петербурге составит 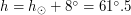 .
. - В далеком будущем для освещения участка поверхности Марса на ареоцентрическую (с центром в центре Марса) стационарную орбиту был выведен спутник с массой, равной 1 тонне, на котором был установлен постоянно работающий прожектор мощностью 10 МВт, узкий луч которого был направлен вниз, на поверхность Марса. Однако оказалось, что для того, чтобы спутник с прожектором совершал один оборот ровно за одни марсианские сутки (24 часа 37 минут), радиус его орбиты необходимо уменьшить по сравнению с обычным радиусом стационарной орбиты. Насколько потребовалось уменьшить радиус орбиты?
Решение: Начнем с выяснения, почему радиус орбиты спутника с прожектором вообще должен быть меньше при том же периоде. Так как на спутнике установлен направленный прожектор, то спутник представляет собой <<фотонную ракету>> (хотя и очень малой мощности), двигатель которой постоянно включен и придает спутнику дополнительное ускорение вверх, вследствие чего эффективное ускорение силы тяжести для спутника оказывается меньше, чем обычное. Ускорение при движении по круговой орбите может быть вычислено как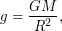 где
где 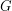 - гравитационная постоянная,
- гравитационная постоянная, 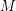 - масса Марса,
- масса Марса, 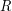 - радиус орбиты. Так как изменения ускорения и радиуса орбиты малы, можно вычислить дифференциалы обеих частей равенства. При малом изменении радиуса орбиты
- радиус орбиты. Так как изменения ускорения и радиуса орбиты малы, можно вычислить дифференциалы обеих частей равенства. При малом изменении радиуса орбиты 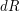 изменение ускорения составит
изменение ускорения составит 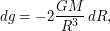 или
или 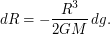 Отметим, что аналогичный результат можно получить и без использования дифференциалов, однако запись промежуточных выкладок станет более громоздкой. Изменение ускорения
Отметим, что аналогичный результат можно получить и без использования дифференциалов, однако запись промежуточных выкладок станет более громоздкой. Изменение ускорения 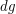 можно получить следующим образом. Каждый фотон с энергией
можно получить следующим образом. Каждый фотон с энергией 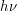 (
( - частота фотона,
- частота фотона, 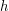 - постоянная Планка), покинувший прожектор, придает прожектору импульс
- постоянная Планка), покинувший прожектор, придает прожектору импульс 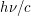 , направленный в сторону, противоположную направлению вылета фотонов (
, направленный в сторону, противоположную направлению вылета фотонов ( - скорость света). Если мощность излучения прожектора
- скорость света). Если мощность излучения прожектора 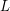 , то за единицу времени прожектор получит импульс
, то за единицу времени прожектор получит импульс 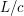 , а импульс, переданный телу за единицу времени - это сила, которая на него действует. Т.о. соответствующее ускорение
, а импульс, переданный телу за единицу времени - это сила, которая на него действует. Т.о. соответствующее ускорение 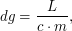 где
где 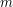 - масса спутника с прожектором. Осталось вычислить выражение
- масса спутника с прожектором. Осталось вычислить выражение 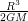 для ареостационарной орбиты. Записывая для нее III закон Кеплера
для ареостационарной орбиты. Записывая для нее III закон Кеплера 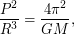 получаем, что
получаем, что 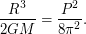 Итоговое выражение имеет вид:
Итоговое выражение имеет вид: 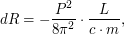 при подстановке данных получаем численный ответ: разность радиусов орбит составляет примерно 3 км.
при подстановке данных получаем численный ответ: разность радиусов орбит составляет примерно 3 км. - Анализ спектра звезды позволил определить ее эффективную температуру
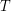 и ускорение силы тяжести на поверхности
и ускорение силы тяжести на поверхности 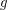 . Из наблюдений известны также видимая звездная величина звезды
. Из наблюдений известны также видимая звездная величина звезды 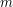 и годичный параллакс
и годичный параллакс 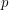 (в угловых секундах). Как, имея эти данные, определить массу звезды?
(в угловых секундах). Как, имея эти данные, определить массу звезды?
Решение: Ускорение силы тяжести на поверхности звезды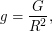 где
где  - масса звезды,
- масса звезды, 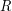 - ее радиус,
- ее радиус, 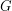 - гравитационная постоянная. Отсюда
- гравитационная постоянная. Отсюда 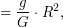 и для решения задачи надо найти радиус звезды. Известно, что светимость звезды
и для решения задачи надо найти радиус звезды. Известно, что светимость звезды 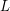 можно записать как
можно записать как 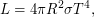 где
где  - постоянная Стефана-Больцмана, и задача сводится к нахождению светимости. По формуле Погсона отношение светимостей звезды
- постоянная Стефана-Больцмана, и задача сводится к нахождению светимости. По формуле Погсона отношение светимостей звезды 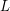 и Солнца
и Солнца 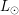 (светимость Солнца равна
(светимость Солнца равна 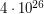 Вт) равно
Вт) равно 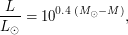 где
где 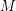 - абсолютная звездная величина звезды,
- абсолютная звездная величина звезды, 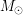 - абсолютная звездная величина Солнца (примерно равная
- абсолютная звездная величина Солнца (примерно равная 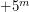 ). Далее пользуемся соотношением между видимой и абсолютной звездными величинами
). Далее пользуемся соотношением между видимой и абсолютной звездными величинами 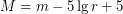 , где
, где  - расстояние до звезды в парсеках. Последнее находим из равенства
- расстояние до звезды в парсеках. Последнее находим из равенства 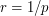 . Собирая все вместе, получаем окончательный результат:
. Собирая все вместе, получаем окончательный результат: 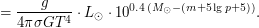
- Облако в межзвездной среде, состоящее из атомарного водорода, имеет максимальную лучевую концентрацию атомов
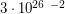 (количество атомов, находящихся в <<столбе>> с основанием
(количество атомов, находящихся в <<столбе>> с основанием 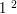 ). Облако имеет форму шара, плотность газа в облаке везде одинакова. При наблюдении облака на длине волны 21 см обнаружилось, что ширина спектральной линии составляет
). Облако имеет форму шара, плотность газа в облаке везде одинакова. При наблюдении облака на длине волны 21 см обнаружилось, что ширина спектральной линии составляет 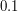 мм. Оцените массу облака.
мм. Оцените массу облака.
Решение: Ширина спектральной линии позволяет найти характерную скорость движения атомов в облаке. Линия расширяется из-за допплеровского смещения, поэтому
движения атомов в облаке. Линия расширяется из-за допплеровского смещения, поэтому 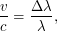 где
где  - скорость света (
- скорость света (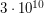 см/с),
см/с), 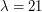 см,
см, 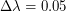 мм (половина ширины линии). Отсюда получаем
мм (половина ширины линии). Отсюда получаем 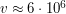 см/с. Найти связь между характерной скоростью и массой облака можно двумя способами. Наиболее корректный - воспользоваться теоремой вириала. Известно, что для устойчивой самогравитирующей системы сумма удвоенной средней кинетической энергии и средней потенциальной энергии равна нулю. Предполагая, что все атомы облака имеют скорость
см/с. Найти связь между характерной скоростью и массой облака можно двумя способами. Наиболее корректный - воспользоваться теоремой вириала. Известно, что для устойчивой самогравитирующей системы сумма удвоенной средней кинетической энергии и средней потенциальной энергии равна нулю. Предполагая, что все атомы облака имеют скорость  , и зная, что потенциальная энергия однородного гравитирующего шара массы
, и зная, что потенциальная энергия однородного гравитирующего шара массы 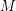 и радиуса
и радиуса 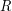 равна
равна 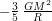 (
(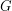 - гравитационная постоянная), получаем равенство:
- гравитационная постоянная), получаем равенство: 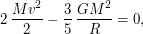 откуда
откуда 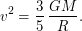 Можно воспользоваться и более простыми соображениями. Все частицы облака движутся по некоторым орбитам вокруг центра облака. Очевидно, что максимальную скорость будут иметь частицы, находящиеся на границе облака, причем их скорость можно приближенно оценить как круговую скорость движения вокруг массы
Можно воспользоваться и более простыми соображениями. Все частицы облака движутся по некоторым орбитам вокруг центра облака. Очевидно, что максимальную скорость будут иметь частицы, находящиеся на границе облака, причем их скорость можно приближенно оценить как круговую скорость движения вокруг массы 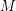 на орбите радиуса
на орбите радиуса 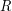 . Тогда
. Тогда 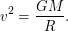 Видно, что результат отличается от предыдущего близким к единице множителем, что для итоговой оценки не слишком существенно. Максимальной лучевая концентрация
Видно, что результат отличается от предыдущего близким к единице множителем, что для итоговой оценки не слишком существенно. Максимальной лучевая концентрация 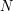 будет в центре облака, причем ее можно выразить как
будет в центре облака, причем ее можно выразить как 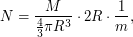 где
где 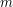 - масса атома водорода (лучевая концентрация - это количество атомов в <<столбе>>, а не масса в нем же). Выразив из этого соотношения и формулы для скорости частиц (для определенности воспользуемся первым вариантом) массу облака, получим
- масса атома водорода (лучевая концентрация - это количество атомов в <<столбе>>, а не масса в нем же). Выразив из этого соотношения и формулы для скорости частиц (для определенности воспользуемся первым вариантом) массу облака, получим 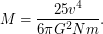 Подставляя числовые данные (масса атома водорода
Подставляя числовые данные (масса атома водорода 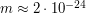 г), получаем ответ:
г), получаем ответ: 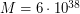 г, что примерно равно
г, что примерно равно 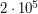 масс Солнца.
масс Солнца. - В результате выполненных в 1979 году измерений скорости расширения известного объекта остатка вспышки сверхновой Кассиопея А (Cas A) было получено, что остаток расширялся со скоростью
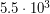 км/с. Измерения 2009 года показали, что тот же остаток расширяется со скоростью
км/с. Измерения 2009 года показали, что тот же остаток расширяется со скоростью 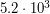 км/с. В каком году вспыхнула эта сверхновая?
км/с. В каком году вспыхнула эта сверхновая?
Решение: Для решения задачи необходимо получить зависимость скорости расширения остатка от времени. Очевидно, что скорость расширения остатка очень велика. Размеры остатков вспышек сверхновых также велики, поэтому можно считать, что на расширение остатка практически не влияет гравитация. Расширение остатка - это разлет продуктов сильного взрыва во внешней среде, и мы можем полагать, что динамика этого разлета определяется энергией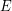 , выделившейся при взрыве, а также плотностью внешней среды
, выделившейся при взрыве, а также плотностью внешней среды 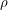 . Попробуем найти формулу, связывающую скорость разлета остатка
. Попробуем найти формулу, связывающую скорость разлета остатка  , время
, время 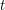 , прошедшее с момента взрыва, а также энергию
, прошедшее с момента взрыва, а также энергию 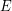 и плотность
и плотность 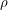 . Для этого воспользуемся методом размерностей: если формула, связывающая эти величины, существует, то ее можно представить в виде
. Для этого воспользуемся методом размерностей: если формула, связывающая эти величины, существует, то ее можно представить в виде 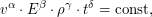 где
где  ,
, 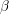 ,
, 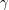 и
и 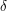 - некоторые числа, а константа в правой части безразмерна. Обозначим размерность длины
- некоторые числа, а константа в правой части безразмерна. Обозначим размерность длины 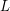 , размерность массы
, размерность массы 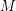 , а размерность времени
, а размерность времени 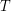 . Тогда все четыре величины имеют следующие размерности:
. Тогда все четыре величины имеют следующие размерности: ![$ [v] = L/T $](/files/tex/4d7ff3050e8c2fbf5224c62acef2bf31d3aa41a3.png) ,
, ![$ [E] = ML^2/T^2 $](/files/tex/37147fdb31e95f71f9f858ea445c4f64c4d7f0ab.png) ,
, ![$ [\rho] = M/L^3 $](/files/tex/0b99145c473c1f01b4c920b10f5bbc898d67677a.png) ,
, ![$ [t]=T $](/files/tex/09dabc278e21e5734700f0791b56bc6053ebde46.png) , а искомая формула, в которой размерности слева и справа должны совпадать, превращается в
, а искомая формула, в которой размерности слева и справа должны совпадать, превращается в 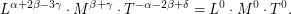 Отсюда получаем систему уравнений:
Отсюда получаем систему уравнений: 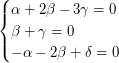 От возведения искомой формулы в произвольную степень ничего не изменится, поэтому одно из четырех неизвестных в системе мы можем выбрать произвольным образом. Пусть, например,
От возведения искомой формулы в произвольную степень ничего не изменится, поэтому одно из четырех неизвестных в системе мы можем выбрать произвольным образом. Пусть, например, 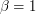 . Тогда
. Тогда 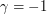 ,
, 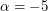 ,
, 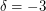 , а искомая зависимость имеет вид
, а искомая зависимость имеет вид 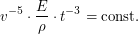 Нас интересует в основном зависимость между скоростью и временем, поэтому мы можем заключить, что
Нас интересует в основном зависимость между скоростью и временем, поэтому мы можем заключить, что 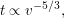 причем время
причем время 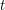 отсчитывается от момента вспышки сверхновой. Тогда, если вспышка произошла
отсчитывается от момента вспышки сверхновой. Тогда, если вспышка произошла 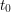 лет назад (считая от 2009 года), можно записать, что
лет назад (считая от 2009 года), можно записать, что 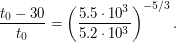 Вычисляем правую часть равенства:
Вычисляем правую часть равенства: 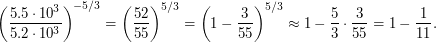 Тогда
Тогда 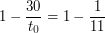 и
и 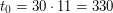 лет. Следовательно, вспышка произошла примерно 330 лет назад, т.е. ориентировочно в 1679 году. Сейчас эта сверхновая известна как <<Сверхновая Флемстида>> - по-видимому, ее в 1680 г. наблюдал первый директор Гринвичской обсерватории Джон Флемстид, однако даже в максимуме блеска объект был слабым (примерно
лет. Следовательно, вспышка произошла примерно 330 лет назад, т.е. ориентировочно в 1679 году. Сейчас эта сверхновая известна как <<Сверхновая Флемстида>> - по-видимому, ее в 1680 г. наблюдал первый директор Гринвичской обсерватории Джон Флемстид, однако даже в максимуме блеска объект был слабым (примерно 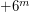 ) и никакого интереса у астрономов не вызвал.
) и никакого интереса у астрономов не вызвал.
Комментарии
8 недель 3 дня назад
8 недель 3 дня назад
9 недель 5 дней назад
12 недель 1 день назад
12 недель 2 дня назад
15 недель 2 дня назад
15 недель 2 дня назад
20 недель 4 дня назад
20 недель 4 дня назад
24 недели 8 часов назад