- Новости
-
Олимпиада
- Рекомендуемая литература
- Положение об олимпиаде
- Методическая программа
- Регламент олимпиады
- Критерии оценивания
- Места проведения олимпиады
- История олимпиады
- Текущая олимпиада
- 2023-2024 учебный год
- 2022-2023 учебный год
- 2021-2022 учебный год
- 2020-2021 учебный год
- 2019-2020 учебный год
- 2018-2019 учебный год
- 2017-2018 учебный год
- 2016-2017 учебный год
- 2015-2016 учебный год
- 2014-2015 учебный год
- 2013-2014 учебный год
- 2012-2013 учебный год
- 2011-2012 учебный год
- 2010-2011 учебный год
- 2009-2010 учебный год
- 2008-2009 учебный год
- 2007-2008 учебный год
- Прочее
- Астрономические кружки
- Летние школы
- Абитуриенту
- Форум
- Ссылки
Условия и решения задач первого тура XV Санкт-Петербургской олимпиады по астрономии (6-7 классы)
1. Условие: На каких широтах Земли человек может в полдень не отбрасывать тени? Почему?
Решение: Человек (как и любые другие предметы) не отбрасывает тени тогда, когда Солнце стоит в зените (т.е. прямо над головой). Из курса географии известно, что Солнце бывает в зените в полдень на широтах от 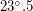 северной широты до
северной широты до 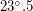 южной широты, т.е. между северным и южным тропиками (включая сами тропики). Однако, человек может не отбрасывать в полдень тени еще и тогда, когда Солнца в полдень вовсе нет на небе. А такое бывает во время полярной ночи на широтах от
южной широты, т.е. между северным и южным тропиками (включая сами тропики). Однако, человек может не отбрасывать в полдень тени еще и тогда, когда Солнца в полдень вовсе нет на небе. А такое бывает во время полярной ночи на широтах от 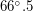 до
до 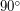 северной широты и от
северной широты и от 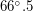 до
до 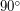 южной широты (т.е. между полярными кругами и полюсами в обоих полушариях).
южной широты (т.е. между полярными кругами и полюсами в обоих полушариях).
2. Условие: В книге Д.Дефо "Жизнь и удивительные приключения Робинзона Крузо" утверждается, что 30 сентября 1659 года, когда, как писал автор, "...нога моя впервые ступила на ужасный остров...", была пятница. Докажите, что автор ошибся и найдите правильный день недели, соответствующий этой дате. Учтите, что в 1659 году в Англии использовался юлианский календарь.
Решение: К сожалению, сделать весь комплект задач олимпиады без единого ляпа, наверное, почти невозможно. В этом году ляп случился в этой задаче. Как выяснилось, ошибся не Даниель Дефо, а автор задачи, который почему-то решил задачу для 30... октября 1659 года. А 30 сентября 1659 года действительно была пятница.
Таким образом, в этой задаче оценивается только сам ход решения, позволяющий выяснить день недели. Сделать это можно так:
Так как требуется найти день недели по юлианскому календарю, то решать задачу проще, используя именно юлианский календарь. Как известно, сейчас разница между юлианским и григорианским календарем составляет 13 суток, поэтому так как в день тура, 8 февраля, по григорианскому календарю была пятница, то по юлианскому календарю пятницей будет 26 января 2008 года.
Выясним, сколько дней отделяют 26 января от 30 сентября. В январе 31 день, в феврале 29 дней (год високосный), в марте - 31, в апреле - 30, мае - 31, июне - 30, июле и августе - по 31. Складывая, получаем 248 дней. Поделив это число с остатком на 7, получаем, что остаток равен 3, поэтому 30 сентября 2008 года - понедельник (по юлианскому календарю). Из этого и будем исходить.
Решим вспомогательную задачу: через какое число лет дни недели, соответствующие некоторой дате, начинают повторяться? Если бы в календаре не было високосных годов, то, очевидно, такое повторение случилось бы через 7 лет (числа 7 и 365 - взаимно простые, поэтому в течение 7-летнего цикла эта дата приходилась бы по одному разу на каждый из семи дней недели). Но каждый 4-й год - високосный, он на 1 сутки длиннее, поэтому итоговая продолжительность цикла составляет 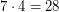 лет. Этот же вывод можно получить, рассуждая так: у нас есть семь возможных дней недели для даты и 4 возможных "типа" года (високосный, 1-й, 2-й и 3-й после високосного), всего возможных комбинаций дня недели и типа года 28, после этого все должно повторяться.
лет. Этот же вывод можно получить, рассуждая так: у нас есть семь возможных дней недели для даты и 4 возможных "типа" года (високосный, 1-й, 2-й и 3-й после високосного), всего возможных комбинаций дня недели и типа года 28, после этого все должно повторяться.
Поделив 2008 на 28 с остатком, получаем в остатке 20. Аналогичная операция с 1659 даст в остатке 7. Эти остатки можно считать номерами годов в 28-летнем цикле. Получается, что 1659 год "устроен так же", как 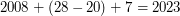 год.
год.
Поделив 365 и 366 с остатком на 7, обнаруживаем, что остатки равны 1 и 2 соответственно. Отсюда следует, что за один обычный год день недели, соответствующий какой-то дате, сдвигается на один вперед, а в високосный год (после 29 февраля) - на два вперед. Поэтому 30 сентября 2009 года по юлианскому календарю будет вторником, оно же 2010 года - средой, оно же 2011 года - четвергом, оно же 2012 года - субботой (2012 год високосный) и т.д. В итоге получаем, что 30 сентября 2023 года (и 30 сентября 1659 года) по юлианскому календарю - пятница.
3. Условие: На какой планете Солнечной системы "Заполярье" (область планеты, на которой возможны полярные дни и полярные ночи) занимает наибольшую площадь? Обоснуйте ответ.
Решение: Как известно, характер освещения Солнцем поверхности планеты зависит от наклона оси вращения планеты к ее орбите. Наглядная иллюстрация этого утверждения видна на рисунке.

Если наклон оси вращения планеты к орбите равен 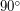 (рис. а), то каждые сутки на всей поверхности планеты ровно половину суток будет длиться ночь, половину - день. Можно сказать, что на такой планете будет вечное равноденствие. Полярного дня или полярной ночи (дня или ночи, продолжающихся непрерывно в течение одних или более суток) не будет на такой планете нигде, может быть за исключением самих полюсов. Соответственно, "Заполярья" на такой планете просто нет (его площадь равна нулю). Если угол наклона немного отличается от
(рис. а), то каждые сутки на всей поверхности планеты ровно половину суток будет длиться ночь, половину - день. Можно сказать, что на такой планете будет вечное равноденствие. Полярного дня или полярной ночи (дня или ночи, продолжающихся непрерывно в течение одних или более суток) не будет на такой планете нигде, может быть за исключением самих полюсов. Соответственно, "Заполярья" на такой планете просто нет (его площадь равна нулю). Если угол наклона немного отличается от 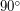 , то "Заполярье" будет, но площадь его будет невелика. Таким образом вращаются Меркурий, Юпитер и Венера.
, то "Заполярье" будет, но площадь его будет невелика. Таким образом вращаются Меркурий, Юпитер и Венера.
Если наклон оси вращения планеты к ее орбите не равен ни 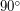 , ни
, ни 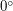 (рис. б и в), то полярные дни и ночи возможны в приполярных областях, причем широты полярных кругов равны углу наклона оси к орбите (например, земная ось наклонена к орбите Земли на
(рис. б и в), то полярные дни и ночи возможны в приполярных областях, причем широты полярных кругов равны углу наклона оси к орбите (например, земная ось наклонена к орбите Земли на 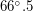 , поэтому северный и южный полярные круги расположены на широтах
, поэтому северный и южный полярные круги расположены на широтах 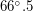 с.ш. и
с.ш. и 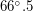 ю.ш., соответственно). Так что, чем меньше угол наклона оси к орбите, тем на более низких широтах располагаются полярные круги и тем больше площадь планеты, занятая "Заполярьем" (сравните рис. б, где ось планеты наклонена под углом
ю.ш., соответственно). Так что, чем меньше угол наклона оси к орбите, тем на более низких широтах располагаются полярные круги и тем больше площадь планеты, занятая "Заполярьем" (сравните рис. б, где ось планеты наклонена под углом 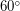 и рис. в, где под углом
и рис. в, где под углом 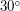 ). Оси вращения планет Земля, Марс, Сатурн и Нептун наклонены к их орбитам на угол около
). Оси вращения планет Земля, Марс, Сатурн и Нептун наклонены к их орбитам на угол около 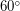 .
.
И, наконец, если ось вращения планеты лежит в плоскости ее орбиты (угол наклона равен 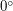 , рис. г), то полярный день и полярная ночь будут охватывать (попеременно) всю поверхность планеты (ровно на половине планеты полярный день, на половине - полярная ночь), за исключением, может быть, экватора. Полярные круги сливаются и "Заполярьем" становится вся планета.
, рис. г), то полярный день и полярная ночь будут охватывать (попеременно) всю поверхность планеты (ровно на половине планеты полярный день, на половине - полярная ночь), за исключением, может быть, экватора. Полярные круги сливаются и "Заполярьем" становится вся планета.
Таким образом, наибольшую площадь "Заполярье" имеет на планете, наклон оси вращения которой к ее орбите наименьший. В Солнечной системе такой планетой является Уран, ось вращения которого парктически лежит в плоскости его орбиты (наклон около 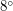 ). Только в узкой экваториальной области Урана регулярно (с периодичностью его вращения) восходит и заходит Солнце, а на всей остальная поверхность планеты бывают полярные дни и ночи различной длительности.
). Только в узкой экваториальной области Урана регулярно (с периодичностью его вращения) восходит и заходит Солнце, а на всей остальная поверхность планеты бывают полярные дни и ночи различной длительности.
4. Условие: В нашей Галактике звезды спектрального класса В "рождаются" примерно раз в 50 лет. Оцените, сколько сейчас таких звезд в Галактике, если продолжительность жизни одной такой звезды составляет 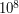 лет.
лет.
Примечание. Число 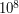 - это единица с 8-ю нулями -
- это единица с 8-ю нулями - 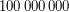 (или сто миллионов).
(или сто миллионов).
Решение: Пусть в какой-то момент в Галактике "родилась" первая звезда спектрального класса В. Она будет жить 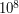 лет. И на протяжении всей ее жизни каждые 50 лет будет рождаться следующая такая же звезда, т.е. через 50 лет таких звезд будет уже две, через 100 лет - 3, через 150 - 4, через 200 - 5 и так далее. Видно, что число звезд через
лет. И на протяжении всей ее жизни каждые 50 лет будет рождаться следующая такая же звезда, т.е. через 50 лет таких звезд будет уже две, через 100 лет - 3, через 150 - 4, через 200 - 5 и так далее. Видно, что число звезд через 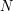 лет равно
лет равно 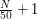 . Однако по прошествии
. Однако по прошествии 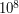 лет первая родившаяся звезда прекратит свое существование, поэтому, вычисляя число звезд, можно просто делить прошедшее время на 50 лет и не заботиться о прибавлении к результату единицы (к тому же числа в задаче даны приближенные, поэтому и вычисления должны выполняться с той же точностью, с какой заданы числа). Таким образом в Галактике по прошествии
лет первая родившаяся звезда прекратит свое существование, поэтому, вычисляя число звезд, можно просто делить прошедшее время на 50 лет и не заботиться о прибавлении к результату единицы (к тому же числа в задаче даны приближенные, поэтому и вычисления должны выполняться с той же точностью, с какой заданы числа). Таким образом в Галактике по прошествии 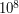 лет будет примерно
лет будет примерно
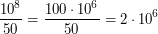
или 2 миллиона звезд. Далее, примерно каждые 50 лет будет и "рождаться", и "умирать" одна звезда, так что среднее количество звезд спектрального класса В будет в Галактике постоянным, если не будет изменяться скорость рождения таких звезд (по крайней мере, на протяжении последних 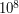 лет). Но указаний на это в условии задачи нет, поэтому ответ таков: в нашей Галактике сейчас примерно два миллиона звезд спектрального класса В.
лет). Но указаний на это в условии задачи нет, поэтому ответ таков: в нашей Галактике сейчас примерно два миллиона звезд спектрального класса В.
5. Условие: На некоторый момент времени для Солнца было получено число Вольфа, которое оказалось равным 180. Считая, что только 30% пятен входило в группы по 3 пятна в каждой, найдите количество пятен в этот момент.
Примечание. Число Вольфа выражается следующей формулой:
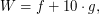
где 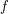 - количество пятен (как входящих в группы по несколько пятен, так и одиночных), а
- количество пятен (как входящих в группы по несколько пятен, так и одиночных), а 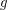 - количество групп пятен. Одиночное пятно также считается группой.
- количество групп пятен. Одиночное пятно также считается группой.
Решение: Число Вольфа 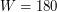 . Число пятен
. Число пятен 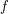 - неизвестно. Но известно, что в группы по три входит 30% пятен, поэтому количество пятен, входящих в группы по три, равно
- неизвестно. Но известно, что в группы по три входит 30% пятен, поэтому количество пятен, входящих в группы по три, равно 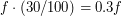 . Тогда число групп по три пятна, очевидно, равно
. Тогда число групп по три пятна, очевидно, равно 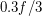 . Количество одиночных пятен равно
. Количество одиночных пятен равно 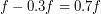 . Тогда количество групп
. Тогда количество групп 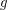 (включая "группы" по одному пятну) равно
(включая "группы" по одному пятну) равно 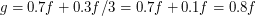 . Отсюда, число Вольфа
. Отсюда, число Вольфа 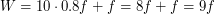 . Так как
. Так как 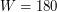 , то
, то 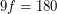 . Отсюда,
. Отсюда, 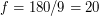 . Так что в описываемый момент на Солнце было 20 пятен, 6 из которых составляли две группы по три пятна.
. Так что в описываемый момент на Солнце было 20 пятен, 6 из которых составляли две группы по три пятна.
| Вложение | Размер |
|---|---|
| Условия и решения задач первого тура (6-7 классы) | 270.24 КБ |
Комментарии
7 недель 4 дня назад
7 недель 4 дня назад
8 недель 6 дней назад
11 недель 3 дня назад
11 недель 3 дня назад
14 недель 4 дня назад
14 недель 4 дня назад
19 недель 5 дней назад
19 недель 5 дней назад
23 недели 1 день назад