- Новости
-
Олимпиада
- Рекомендуемая литература
- Положение об олимпиаде
- Методическая программа
- Регламент олимпиады
- Критерии оценивания
- Места проведения олимпиады
- История олимпиады
- Текущая олимпиада
- 2023-2024 учебный год
- 2022-2023 учебный год
- 2021-2022 учебный год
- 2020-2021 учебный год
- 2019-2020 учебный год
- 2018-2019 учебный год
- 2017-2018 учебный год
- 2016-2017 учебный год
- 2015-2016 учебный год
- 2014-2015 учебный год
- 2013-2014 учебный год
- 2012-2013 учебный год
- 2011-2012 учебный год
- 2010-2011 учебный год
- 2009-2010 учебный год
- 2008-2009 учебный год
- 2007-2008 учебный год
- Прочее
- Астрономические кружки
- Летние школы
- Абитуриенту
- Форум
- Ссылки
Условия и решения задач районного тура (8-9 классы) XV Санкт-Петербургской олимпиады по астрономии
- Условие: Козерог, Дракон, Рыбы, Лев, Змееносец, Рак. Найдите лишнее в этом списке. Обоснуйте свой ответ. Решение: Лишнее в этом списке - созвездие Дракона, это единственное созвездие, не лежащее на эклиптике (видимом пути Солнца на небесной сфере в течение года). Распространенное заблуждение, что Змееносец - незодиакальное созвездие, основано на странной, мягко говоря, астрологической традиции, в соответствии с которой в качестве "знаков Зодиака" выбраны только 12 созвездий из 13, находящихся на эклиптике.
- Условие: В одной из телепередач, посвященных жизни и творчеству А.С.Пушкина, ведущая передачи Фекла Толстая заявила, что существует "... до сих пор не разгаданная загадка, связанная с жизнью поэта". Загадка состояла в следующем: Известно, что А.С.Пушкин родился 26 мая. Всем известно, что разница между старым и новым стилем составляет 13 дней. Однако мы празднуем день рождения Пушкина (по новому стилю) 6 июня, хотя разница между 26 мая и 6 июня - всего 11 дней. Внесите свой вклад в литературоведение - разгадайте загадку. Сегодня (8.12.2007) в то же время проходит первый тур городской олимпиады по литературе. Оргкомитет олимпиады надеется, что эта задача послужит некоторым утешением для тех, кто, выбирая между астрономией и литературой, выбрал астрономию. Решение: Юлианский и григорианский календари ("старый стиль" и "новый стиль" соответственно) отличаются тем, что годы, номера которых делятся на 100 и не делятся на 400, в юлианском календаре являются високосными, а в григорианском - нет. Поэтому пересчет дат различных событий из юлианского календаря в григорианский не всегда производится прибавлением 13 суток - так следует делать только для событий, произошедших после 1 марта 1900 года и до 28 февраля 2099 года (по григорианскому календарю). При пересчете дат, относящихся к XVIII веку, из юлианского календаря в григорианский, следует прибавлять не 13, а 11 дней - с тех пор разница между юлианским и григорианским календарями увеличилась на 2 дня (один день появился в 1800 году, второй - в 1900 году). Именно поэтому день рождения А.С.Пушкина, родившегося в 1799 году, празднуется 6 июня, а не 8 июня.
- Условие: Сегодня в Петербурге Солнце взошло в 9 часов 48 минут, а в Москве в 8 часов 48 минут. Заход же Солнца в Петербурге и в Москве произойдет практически в одно и то же время - в 15 часов 58 минут. Почему моменты восхода различаются, а моменты захода совпадают? Решение: Разная продолжительность светового дня в Петербурге и Москве объясняется тем, что эти города находятся на разных широтах. Петербург севернее Москвы, поэтому зимой продолжительность дня в Петербурге меньше. "Несимметричность" уменьшения продолжительности светового дня обусловлена тем, что Петербург и Москва, хотя и находятся в одном часовом поясе, расположены на существенно разных долготах. Москва восточнее Петербурга, поэтому моменты восхода и захода в Москве при прочих равных условиях наступают раньше, чем в Петербурге. В итоге и первый, и второй фактор сдвигают время восхода в Москве по сравнению с Петербургом вперед (на более ранний момент времени), а вот время захода первый фактор сдвигает назад, а второй - вперед, и их влияние компенсируется.
-
Условие: Пассажир, летящий на самолете из Сургута в Санкт-Петербург, заметил, что в течение всего перелета Луна практически не меняла своей высоты над горизонтом. Оцените скорость, с которой летел самолет. Широта Санкт-Петербурга и Сургута примерно одинакова -
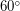 .
.
 Решение: Поскольку Луна при наблюдении с самолета практически не меняла своей высоты над горизонтом, можно считать, что угловая скорость движения самолета примерно равна угловой скорости движения Луны. За угловую скорость движения Луны можно принять угловую скорость вращения Земли -
Решение: Поскольку Луна при наблюдении с самолета практически не меняла своей высоты над горизонтом, можно считать, что угловая скорость движения самолета примерно равна угловой скорости движения Луны. За угловую скорость движения Луны можно принять угловую скорость вращения Земли - 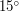 в час. При этом приходится пренебрегать собственным движением Луны, связанным с обращением Луны вокруг Земли, но в оценочной задаче такое пренебрежение допустимо (т.к. собственное движение Луны (
в час. При этом приходится пренебрегать собственным движением Луны, связанным с обращением Луны вокруг Земли, но в оценочной задаче такое пренебрежение допустимо (т.к. собственное движение Луны (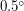 в час) примерно в 30 раз меньше, чем угловая скорость вращения Земли - во столько же раз, во сколько продолжительность суток меньше продолжительности месяца). Если пренебречь высотой полета по сравнению с радиусом Земли и считать, что самолет летел вдоль параллели, то линейная скорость, с которой летел самолет, равна линейной скорости движения вдоль параллели точки земной поверхности вследствие вращения Земли. Длина полной окружности (
в час) примерно в 30 раз меньше, чем угловая скорость вращения Земли - во столько же раз, во сколько продолжительность суток меньше продолжительности месяца). Если пренебречь высотой полета по сравнению с радиусом Земли и считать, что самолет летел вдоль параллели, то линейная скорость, с которой летел самолет, равна линейной скорости движения вдоль параллели точки земной поверхности вследствие вращения Земли. Длина полной окружности (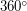 ) равна
) равна 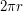 , где
, где  - ее радиус. Если точка земной поверхности проходит за 1 час
- ее радиус. Если точка земной поверхности проходит за 1 час 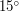 , то за 1 час она проходит линейное расстояние равное
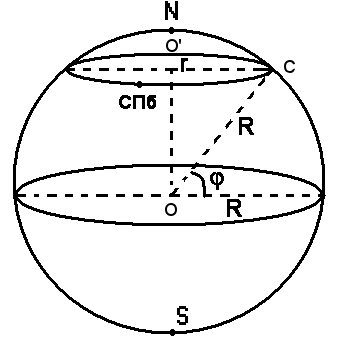
, то за 1 час она проходит линейное расстояние равное 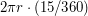 . Так как движение происходит по 60-й параллели, то и радиус надо брать соответствующий (см. рисунок). Радиус 60-й параллели
. Так как движение происходит по 60-й параллели, то и радиус надо брать соответствующий (см. рисунок). Радиус 60-й параллели  можно вычислить из прямоугольного треугольника
можно вычислить из прямоугольного треугольника 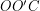 , где гипотенуза
, где гипотенуза 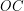 равна
равна 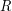 - радиусу Земли, а катет
- радиусу Земли, а катет 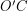 равен
равен  . Угол при вершине
. Угол при вершине 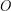 равен
равен 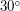 (
(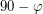 , где
, где 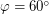 - широта). Тогда
- широта). Тогда  как катет, противолежащий углу в
как катет, противолежащий углу в 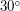 , будет равен половине гипотенузы, т.е.
, будет равен половине гипотенузы, т.е. 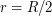 .
. 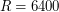 км. Тогда скорость движения самолета равна
км. Тогда скорость движения самолета равна 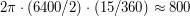 км/час.
км/час.
-
Условие: В некоторой системе физических единиц в качестве основных величин выбраны скорость света (равная "1 скорости света") и диаметр Земли (равный "1 диаметру Земли"). Чему в этой системе единиц равны сутки?
Решение: Обозначим
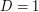 "диаметр Земли",
"диаметр Земли", 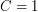 "скорость света".
1 секунду можно представить таким образом:
"скорость света".
1 секунду можно представить таким образом: 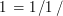 . Оценим теперь, чему равны в нашей системе единиц 1 с и 1 км/c.
Диаметр Земли приближенно равен 12800 км. Отсюда
. Оценим теперь, чему равны в нашей системе единиц 1 с и 1 км/c.
Диаметр Земли приближенно равен 12800 км. Отсюда 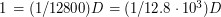 . Скорость света приближенно равна
. Скорость света приближенно равна 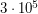 км/с, следовательно,
км/с, следовательно, 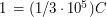 . Поделив одно на другое, получаем величину секунды:
. Поделив одно на другое, получаем величину секунды:
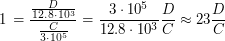 В сутках 86400 с (
В сутках 86400 с (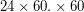 ), следовательно,
), следовательно, 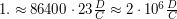 , т.е. сутки в данной системе единиц примерно равны
, т.е. сутки в данной системе единиц примерно равны
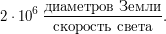
Решения также можно скачать в виде pdf-файла:
| Вложение | Размер |
|---|---|
| Условия и решения задач районного тура (8-9 классы) | 274.93 КБ |
- Войдите или зарегистрируйтесь, чтобы получить возможность отправлять комментарии
Комментарии
6 недель 1 день назад
6 недель 1 день назад
7 недель 3 дня назад
9 недель 6 дней назад
10 недель 16 часов назад
13 недель 20 часов назад
13 недель 21 час назад
18 недель 2 дня назад
18 недель 2 дня назад
21 неделя 5 дней назад