- Новости
-
Олимпиада
- Рекомендуемая литература
- Положение об олимпиаде
- Методическая программа
- Регламент олимпиады
- Критерии оценивания
- Места проведения олимпиады
- История олимпиады
- Текущая олимпиада
- 2023-2024 учебный год
- 2022-2023 учебный год
- 2021-2022 учебный год
- 2020-2021 учебный год
- 2019-2020 учебный год
- 2018-2019 учебный год
- 2017-2018 учебный год
- 2016-2017 учебный год
- 2015-2016 учебный год
- 2014-2015 учебный год
- 2013-2014 учебный год
- 2012-2013 учебный год
- 2011-2012 учебный год
- 2010-2011 учебный год
- 2009-2010 учебный год
- 2008-2009 учебный год
- 2007-2008 учебный год
- Прочее
- Астрономические кружки
- Летние школы
- Абитуриенту
- Форум
- Ссылки
Условия и решения задач первого тура XV Санкт-Петербургской олимпиады по астрономии (8-9 классы)
1. Условие: На краю диска Солнца обнаружен протуберанец, угловой размер которого равен 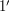 . Оцените его линейные размеры.
. Оцените его линейные размеры.
Решение: Известно, что угловой размер Солнца на небесной сфере составляет примерно 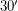 . Так как он достаточно мал, то линейные размеры деталей диска Солнца можно считать пропорциональными их угловым размерам. Поэтому размер протуберанца составляет примерно
. Так как он достаточно мал, то линейные размеры деталей диска Солнца можно считать пропорциональными их угловым размерам. Поэтому размер протуберанца составляет примерно 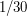 диаметра Солнца, т.е.
диаметра Солнца, т.е. 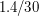 млн.км
млн.км 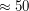 тыс.км.
тыс.км.
2. Условие: В скоплении галактик 100 карликовых эллиптических галактик и одна гигантская эллиптическая галактика. Какую абсолютную звездную величину имеет гигантская галактика, если все карликовые галактики светят так же, как она одна, и абсолютная звездная величина каждой из них 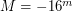 ?
?
Решение: По условию суммарная светимость 100 карликовых галактик равна светимости одной гигантской галактики, поэтому светимость одной карликовой галактики в 100 раз меньше светимости гигантской. Известно, что изменение светимости в 100 раз соответствует изменению абсолютной звездной величины на 5 единиц, поэтому абсолютная звездная величина гигантской галактики 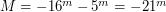 .
.
3. Условие: Известно, что сутки на Земле увеличиваются на 2 мс за 100 лет. Как далеко от нас отстоит та эпоха, в которой юлианский календарь был максимально точен (т.е. год юлианского календаря наиболее близок к тропическому году)? В 1900 году продолжительность тропического года была равна 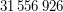 секунд или
секунд или 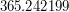 суток.
суток.
Решение: Продолжительность года юлианского календаря равна 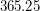 суток. В 1900 году продолжительность тропического года была на
суток. В 1900 году продолжительность тропического года была на 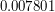 суток меньше. Поскольку продолжительность суток непрерывно увеличивается, то в году их становится меньше, а значит, юлианский календарь был справедлив в прошлом. Определим, как давно.
суток меньше. Поскольку продолжительность суток непрерывно увеличивается, то в году их становится меньше, а значит, юлианский календарь был справедлив в прошлом. Определим, как давно.
Разнице в 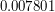 суток соответствует примерно 674 секунды 1900 года (так называемая эфемеридная секунда). Это время должно "набежать" за
суток соответствует примерно 674 секунды 1900 года (так называемая эфемеридная секунда). Это время должно "набежать" за 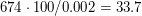 миллионов лет. Это примерно соответствует времени появления на нашей планете первых человекообразных обезьян (середина олигоцена, палеоген, кайнозой).
миллионов лет. Это примерно соответствует времени появления на нашей планете первых человекообразных обезьян (середина олигоцена, палеоген, кайнозой).
4. Условие: В момент прохождения Венерой нижнего соединения наблюдатели на Земле средствами радиолокации построили карту видимого полушария Венеры. В следующее нижнее соединение радиоастрономы снова проводят сеанс радиолокации. На какой угол повернулась картографированная поверхность (любая отмеченная точка на поверхности Венеры) по отношению к зафиксированному в предыдущее соединение положению? Сколько должно пройти нижних соединений, чтобы таким образом построить полную карту Венеры? Венера совершает один оборот вокруг Солнца за 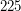 суток, а вокруг оси - за
суток, а вокруг оси - за 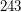 суток.
суток.
Решение: Синодический период Венеры равен
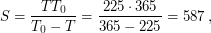
где 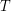 и
и 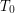 - периоды обращения вокруг Солнца Венеры и Земли соответственно. Величину солнечных суток на Венере можно вычислить из соотношения:
- периоды обращения вокруг Солнца Венеры и Земли соответственно. Величину солнечных суток на Венере можно вычислить из соотношения:
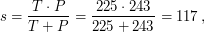
где 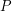 - период вращения Венеры вокруг оси. Отсюда получаем, что за период между двумя прохождениями нижнего соединения, то есть один синодический период на Венере проходит ровно
- период вращения Венеры вокруг оси. Отсюда получаем, что за период между двумя прохождениями нижнего соединения, то есть один синодический период на Венере проходит ровно
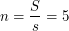
солнечных суток, т.е. Венера каждое нижнее соединение располагается к Земле одной стороной (астрономы говорят, что осевое вращение Венеры находится в резонансе с синодическим периодом Венеры по отношению к Земле). Значит, радиолокацией только в нижнем соединении можно построить карту только одного полушария Венеры, а полную карту поверхности построить нельзя.
5. Условие: Земляне запустили автоматическую межпланетную станцию (АМС) на орбиту Марса. АМС стартовала с земной орбиты и летит к орбите Марса по гомановскому эллипсу (это эллипс, который в перигелии касается орбиты Земли, а в афелии - орбиты Марса). В момент старта с орбиты Земли АМС имела скорость 33 км/с относительно Солнца. Какую скорость необходимо дополнительно придать АМС, когда она достигнет орбиты Марса, чтобы в дальнейшем она стала двигаться по круговой орбите вокруг Солнца?
Решение: Марс находится в 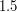 раза дальше от Солнца, чем Земля. Воспользуемся II законом Кеплера ("за равные промежутки времени радиус-вектор планеты заметает равные площади") для АМС в перигелии (на орбите Земли) и в афелии (на орбите Марса).
раза дальше от Солнца, чем Земля. Воспользуемся II законом Кеплера ("за равные промежутки времени радиус-вектор планеты заметает равные площади") для АМС в перигелии (на орбите Земли) и в афелии (на орбите Марса).
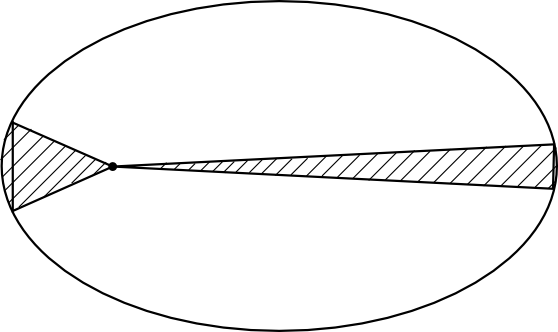
На рисунке заштрихованы площади, пройденные по эллиптической орбите за единицу времени. Площади секторов можно считать приближенно равными площадям соответствующих треугольников. Поскольку время единичное, то основания треугольников (хорды, стягивающие заштрихованные сектора) численно равны скоростям в перигелии и афелии, а высоты треугольников - перигелийное и афелийное расстояния.
Из равенства площадей делаем вывод:
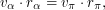
где индексами  обозначены скорость и расстояние в афелии (на орбите Марса), а индексами
обозначены скорость и расстояние в афелии (на орбите Марса), а индексами  - скорость и расстояние в перигелии (на орбите Земли).
- скорость и расстояние в перигелии (на орбите Земли).
В нашем случае известно, что 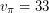 км/с,
км/с, 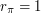 а.е.,
а.е., 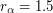 а.е. Отсюда получаем, что
а.е. Отсюда получаем, что 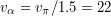 км/с - такую скорость будет иметь АМС, подлетевшая к орбите Марса.
км/с - такую скорость будет иметь АМС, подлетевшая к орбите Марса.
Найдем круговую скорость на орбите Марса. Воспользуемся для этого III законом Кеплера:
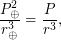
где 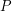 - периоды обращения вокруг Солнца,
- периоды обращения вокруг Солнца,  - радиусы орбит, индексы
- радиусы орбит, индексы 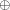 относятся к Земле, а
относятся к Земле, а  - к Марсу. Отсюда
- к Марсу. Отсюда
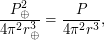
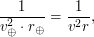
где 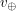 ,
,  - круговые скорости движения по соответствующим орбитам. Известно, что
- круговые скорости движения по соответствующим орбитам. Известно, что 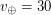 км/с, отсюда
км/с, отсюда
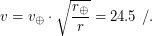
Следовательно, при подлете к орбите Марса АМС требуется придать дополнительную скорость 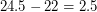 км/с.
км/с.
| Вложение | Размер |
|---|---|
| Условия и решения задач первого тура (8-9 классы) | 259.22 КБ |
Комментарии
7 недель 4 дня назад
7 недель 4 дня назад
8 недель 6 дней назад
11 недель 3 дня назад
11 недель 3 дня назад
14 недель 3 дня назад
14 недель 4 дня назад
19 недель 5 дней назад
19 недель 5 дней назад
23 недели 1 день назад