- Новости
-
Олимпиада
- Рекомендуемая литература
- Положение об олимпиаде
- Методическая программа
- Регламент олимпиады
- Критерии оценивания
- Места проведения олимпиады
- История олимпиады
- Текущая олимпиада
- 2023-2024 учебный год
- 2022-2023 учебный год
- 2021-2022 учебный год
- 2020-2021 учебный год
- 2019-2020 учебный год
- 2018-2019 учебный год
- 2017-2018 учебный год
- 2016-2017 учебный год
- 2015-2016 учебный год
- 2014-2015 учебный год
- 2013-2014 учебный год
- 2012-2013 учебный год
- 2011-2012 учебный год
- 2010-2011 учебный год
- 2009-2010 учебный год
- 2008-2009 учебный год
- 2007-2008 учебный год
- Прочее
- Астрономические кружки
- Летние школы
- Абитуриенту
- Форум
- Ссылки
Условия и решения задач первого тура XV Санкт-Петербургской городской олимпиады по астрономии (10 класс)
1. Условие: В веществе Солнца 70% (по массе) составляет водород, 27% - гелий, 3% - более тяжелые элементы. Оцените среднюю молярную массу вещества Солнца.
Решение: Как известно, молярная масса - это масса в граммах одного моля (т.е. числа Авогадро 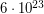 частиц) или (в силу определения моля, так как число Авогадро - величина, обратная атомной единице массы, выраженной в граммах) средняя масса одной частицы в атомных единицах массы (а.е.м.). Именно второй вариант определения нам и понадобится.
частиц) или (в силу определения моля, так как число Авогадро - величина, обратная атомной единице массы, выраженной в граммах) средняя масса одной частицы в атомных единицах массы (а.е.м.). Именно второй вариант определения нам и понадобится.
Практически все вещество Солнца ионизовано. Поэтому водород, входящий в состав Солнца - это не молекулы водорода и даже не атомы, а отдельные ядра и электроны. Тяжелых изотопов водорода на Солнце практически нет, поэтому у водорода на каждую 1 атомную единицу массы приходится две частицы - ядро водорода (протон), масса которого примерно равна 1 а.е.м., и электрон, масса которого пренебрежимо мала (порядка 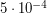 а.е.м.). Поэтому молярная масса ионизованного водорода равна 0.5 г/моль.
а.е.м.). Поэтому молярная масса ионизованного водорода равна 0.5 г/моль.
Выполним аналогичные рассуждения для гелия. Основной изотоп гелия, встречающийся на Солнце - 4He - при ионизации превращается в ядро с массой 4 а.е.м. и два электрона. Молярная масса ионизованного гелия 1.3 г/моль.
Более тяжелыми элементами можно пренебречь. Во-первых, их очень мало, во-вторых, при их ионизации образуется много электронов, поэтому их молярная масса окажется близкой к молярной массе гелия, около 2 г/моль.
Осталось найти среднее. Для простоты (в силу изложенного в предыдущем абзаце) будем считать, что гелия в Солнце 30% по массе, а тяжелых элементов нет вообще. Так как масса атома водорода в 4 раза меньше, чем масса атома гелия, то отношение 7:3 по массе означает, что на каждые 3 атома (вернее, комплекта частиц, из которых можно составить атом) гелия в веществе Солнца имеется 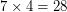 атомов водорода. Получаем, что 28 ядер водорода, 3 ядра гелия и
атомов водорода. Получаем, что 28 ядер водорода, 3 ядра гелия и 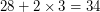 электрона, всего 65 частиц, соответствуют
электрона, всего 65 частиц, соответствуют 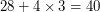 а.е.м. Тогда средняя молярная масса
а.е.м. Тогда средняя молярная масса 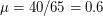 г/моль.
г/моль.
2. Условие: У некоторой звезды лучевая скорость не наблюдается, а собственное движение равно 2''/год На сколько звездных величин изменилась видимая звездная величины звезды за последний миллион лет?
Решение:
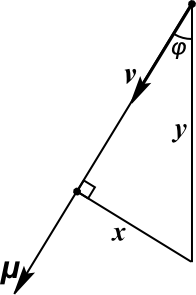
Введем обозначения (см.рисунок):  - расстояние до звезды в настоящее время,
- расстояние до звезды в настоящее время, 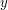 - расстояние до звезды миллион лет назад,
- расстояние до звезды миллион лет назад, 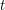 - прошедшее время,
- прошедшее время,  - скорость звезды в пространстве,
- скорость звезды в пространстве, 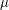 - собственное движение звезды.
- собственное движение звезды.
Мы находимся в правом нижнем углу треугольника, миллион лет назад звезда находилась в верхнем углу треугольника, а сейчас - в левом нижнем углу. Так как лучевая скорость не наблюдается (т.е. пренебрежимо мала), то треугольник прямоугольный - в настоящее время вектор скорости звезды перпендикулярен направлению на звезду.
Расстояние до звезды в настоящее время можно выразить как 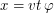 . Так как собственное движение звезды
. Так как собственное движение звезды 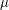 - это (по определению) ее угловая скорость на небесной сфере, то
- это (по определению) ее угловая скорость на небесной сфере, то 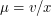 (если
(если 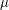 выражена в радианах на единицу времени).
выражена в радианах на единицу времени).
Отсюда получаем
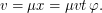
Переводя собственное движение в радианы в год, получаем 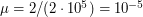 год-1, тогда
год-1, тогда
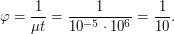
Отношение расстояний до звезды в настоящее время и миллион лет назад 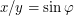 . Поскольку
. Поскольку 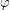 мал, то угол, выраженный в радианах, и синус этого угла примерно равны тангенсу. Следовательно, за прошедшее время расстояние до звезды уменьшилось в 10 раз.
мал, то угол, выраженный в радианах, и синус этого угла примерно равны тангенсу. Следовательно, за прошедшее время расстояние до звезды уменьшилось в 10 раз.
Освещенность, создаваемая звездой, обратно пропорциональна квадрату расстояния. Следовательно, освещенность изменилась в 100 раз, что соответствует изменению видимой звездной величины на 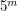 .
.
3. Условие: Космонавт прилетел на астероид, имеющий форму шара, и обошел его по экватору за полтора часа. Оцените массу астероида, если известно, что средняя плотность астероида меньше средней плотности Земли, а космонавт передвигался со средней скоростью пешехода.
Решение: Допустим, что средняя скорость пешехода 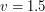 м/с. Так как длина экватора астероида радиуса
м/с. Так как длина экватора астероида радиуса 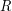 равна
равна 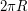 , то отсюда следует, что радиус астероида
, то отсюда следует, что радиус астероида
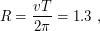
где 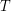 - время, за которое астероид был обойден.
- время, за которое астероид был обойден.
Тем самым мы знаем объем астероида и, умножив его на плотность, можем получить массу. Однако нам известно лишь то, что плотность астероида меньше плотности Земли (т.е. меньше 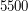 кг/м
кг/м ), и поэтому пока что мы можем получить лишь верхнюю оценку массы. Требуется как-то оценить плотность снизу.
), и поэтому пока что мы можем получить лишь верхнюю оценку массы. Требуется как-то оценить плотность снизу.
Астероид маленький и его масса явно невелика. Поэтому обход пешком такого астероида возможен только в том случае, если скорость пешехода не окажется большей, чем первая космическая скорость (иначе пешеход просто улетит). Отсюда следует, что
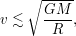
где 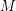 - масса астероида, а
- масса астероида, а 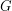 - гравитационная постоянная. Преобразуем неравенство:
- гравитационная постоянная. Преобразуем неравенство:
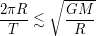
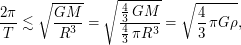
где 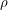 - средняя плотность астероида. Возводя неравенство в квадрат и преобразуя, получаем условие на плотность
- средняя плотность астероида. Возводя неравенство в квадрат и преобразуя, получаем условие на плотность
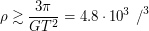
Теперь "вилка" для плотности оказывается достаточно узкой. Подсчитывая массу для минимального и максимального значения плотности, получаем

Отсюда ответ: масса астероида составляет 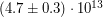 кг.
кг.
4. Условие: В некотором городе в результате засветки неба уличным освещением предельная звездная величина звезд, видимых невооруженным глазом, оказалась равной 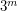 . Оцените поверхностную яркость неба (звездную величину, приходящуюся на квадратную угловую секунду небесной сферы) в этом городе.
. Оцените поверхностную яркость неба (звездную величину, приходящуюся на квадратную угловую секунду небесной сферы) в этом городе.
Решение: Предельное угловое разрешение человеческого глаза составляет около 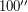 . Поэтому любая звезда видна на небе, вообще говоря, не как точка, а как пятно с характерным угловым размером
. Поэтому любая звезда видна на небе, вообще говоря, не как точка, а как пятно с характерным угловым размером 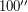 . Площадь такого пятна составляет
. Площадь такого пятна составляет 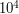 кв.секунд.
кв.секунд.
Будем считать, что для самых слабых видимых звезд поверхностная яркость одной кв.секунды неба должна примерно совпадать с поверхностной яркостью одной кв.секунды звезды. Так как предельная звездная величина по условию равна 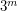 , то поверхностная яркость 1 кв.секунды звезды (и неба) окажется равной
, то поверхностная яркость 1 кв.секунды звезды (и неба) окажется равной 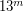 (освещенности, создаваемые "отдельными" квадратными секундами звезды, складываются, а изменение освещенности на 4 порядка соответствует изменению на 10 звездных величин). Это и есть искомая оценка.
(освещенности, создаваемые "отдельными" квадратными секундами звезды, складываются, а изменение освещенности на 4 порядка соответствует изменению на 10 звездных величин). Это и есть искомая оценка.
5. Условие: Угловое расстояние между точками восхода и захода Сириуса составляет 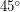 . Определите широту места наблюдения. Экваториальные координаты Сириуса:
. Определите широту места наблюдения. Экваториальные координаты Сириуса: 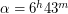 ,
, 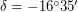
Решение:
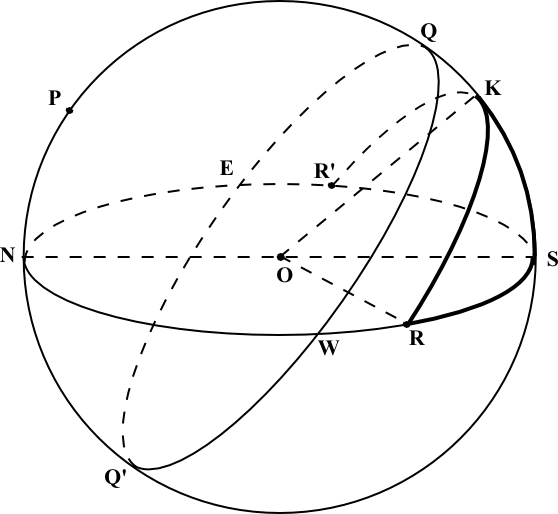
Нарисуем небесную сферу и на ней суточную параллель Сириуса. Суточная параллель Сириуса пересекает горизонт в точках 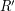 (на восходе) и
(на восходе) и 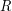 (на заходе), угловое расстояние между которыми (плоский угол
(на заходе), угловое расстояние между которыми (плоский угол 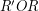 , или дуга
, или дуга 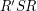 )по условию равно
)по условию равно 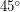 .
.
Рассмотрим сферический треугольник 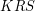 . В нем:
. В нем:
- угол
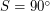 как угол между горизонтом и меридианом;
как угол между горизонтом и меридианом; - угол
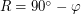 , где
, где 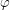 - широта места наблюдения (угол при вершине
- широта места наблюдения (угол при вершине 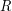 образован плоскостями параллели и горизонта, а значит, равен углу между экватором и горизонтом);
образован плоскостями параллели и горизонта, а значит, равен углу между экватором и горизонтом); - угол
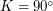 как угол между параллелью и меридианом;
как угол между параллелью и меридианом; - сторона
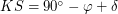 , т.к. это высота Сириуса в верхней кульминации;
, т.к. это высота Сириуса в верхней кульминации; - сторона
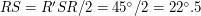
Так как треугольник достаточно малый, можно считать его плоским (те, кто знает сферическую тригонометрию, могут этим приближением не пользоваться, но точность ответа при этом существенно не возрастет). Тогда длины сторон можно выражать в угловой мере (в радианах), считая радиус сферы некоторой константой.
Запишем для этого треугольника теорему синусов:
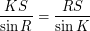
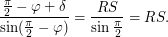
Обозначим 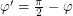 , тогда
, тогда
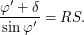
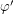 - малый угол, потому
- малый угол, потому 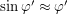 . Тогда
. Тогда
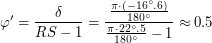
или примерно 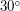 . Тогда
. Тогда 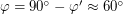 .
.
Примечание. Если пользоваться сферической тригонометрией, то решение выглядит следующим образом.
Теорема синусов:
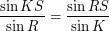
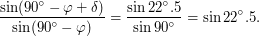
Обозначим 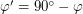 , тогда
, тогда
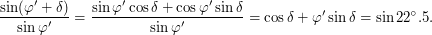
Отсюда
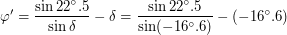
Так как углы достаточно малы, будем считать, что синус угла приближенно равен значению угла в радианах, а косинус приближенно равен единице, тогда
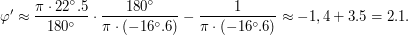
Отсюда 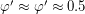 , или
, или 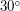 , а
, а 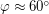 .
.
Если считать "точно" (на калькуляторе), то оказывается, что 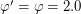 и
и 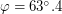 , так что мы не так уж и ошиблись.
, так что мы не так уж и ошиблись.
| Вложение | Размер |
|---|---|
| Условия и решения задач первого тура | 283.75 КБ |
Комментарии
6 недель 4 дня назад
6 недель 4 дня назад
7 недель 6 дней назад
10 недель 2 дня назад
10 недель 3 дня назад
13 недель 3 дня назад
13 недель 3 дня назад
18 недель 5 дней назад
18 недель 5 дней назад
22 недели 1 день назад