- Новости
-
Олимпиада
- Рекомендуемая литература
- Положение об олимпиаде
- Методическая программа
- Регламент олимпиады
- Критерии оценивания
- Места проведения олимпиады
- История олимпиады
- Текущая олимпиада
- 2023-2024 учебный год
- 2022-2023 учебный год
- 2021-2022 учебный год
- 2020-2021 учебный год
- 2019-2020 учебный год
- 2018-2019 учебный год
- 2017-2018 учебный год
- 2016-2017 учебный год
- 2015-2016 учебный год
- 2014-2015 учебный год
- 2013-2014 учебный год
- 2012-2013 учебный год
- 2011-2012 учебный год
- 2010-2011 учебный год
- 2009-2010 учебный год
- 2008-2009 учебный год
- 2007-2008 учебный год
- Прочее
- Астрономические кружки
- Летние школы
- Абитуриенту
- Форум
- Ссылки
Задачи и решения (9 класс)
- Оцените, во сколько раз отличаются скорости низколетящих спутников Земли и Юпитера, если известно, что радиус Юпитера примерно в 10 раз меньше радиуса Солнца.
Решение: Так как спутники низколетящие, то это означает, что орбиты у спутников круговые и радиус орбиты примерно совпадает с радиусом соответствующей планеты. Если обозначить массу планеты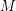 , а радиус
, а радиус 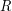 , то ускорение свободного падения для спутника можно вычислить как
, то ускорение свободного падения для спутника можно вычислить как 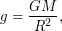 где
где 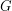 - гравитационная постоянная. Известно, что для кругового движения со скоростью
- гравитационная постоянная. Известно, что для кругового движения со скоростью 
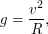 отсюда получаем, что
отсюда получаем, что 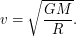 Преобразуем это выражение.
Преобразуем это выражение. 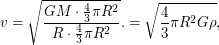 где
где 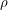 - средняя плотность планеты. Плотности Земли и Юпитера известны - это
- средняя плотность планеты. Плотности Земли и Юпитера известны - это 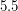 г/см
г/см и
и 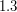 г/см
г/см соответственно (для оценки можно взять 5 и 1), радиус Юпитера можно оценить, зная радиус Солнца (если он неизвестен, то легко "восстанавливается" либо из данных о плотности и массе Солнца (последнюю можно получить, зная радиус орбиты Земли и продолжительность года), либо из данных об угловом размере диска Солнца и расстоянии до него). В итоге оказывается, что радиус Юпитера примерно в 10 раз больше радиуса Земли, и, следовательно, скорость низколетящего спутника Юпитера будет в
соответственно (для оценки можно взять 5 и 1), радиус Юпитера можно оценить, зная радиус Солнца (если он неизвестен, то легко "восстанавливается" либо из данных о плотности и массе Солнца (последнюю можно получить, зная радиус орбиты Земли и продолжительность года), либо из данных об угловом размере диска Солнца и расстоянии до него). В итоге оказывается, что радиус Юпитера примерно в 10 раз больше радиуса Земли, и, следовательно, скорость низколетящего спутника Юпитера будет в 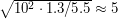 раз больше, чем скорость такого же спутника Земли.
раз больше, чем скорость такого же спутника Земли. - 2 марта этого года астероид 2009 DD45 пролетел между Землей и Луной. Предположим, что астероид в некоторый момент оказался точно на прямой, соединяющей наблюдателя на Земле и центр Луны, двигался со скоростью 20 км/с под углом
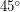 к этой прямой и находился на расстоянии 64 тыс.км от наблюдателя. Найдите время, за которое астероид для наблюдателя пересек диск Луны. Радиус Луны в 4 раза меньше радиуса Земли, расстояние от Земли до Луны равно примерно 60 радиусам Земли.
к этой прямой и находился на расстоянии 64 тыс.км от наблюдателя. Найдите время, за которое астероид для наблюдателя пересек диск Луны. Радиус Луны в 4 раза меньше радиуса Земли, расстояние от Земли до Луны равно примерно 60 радиусам Земли.
Решение: Радиус Земли примерно равен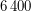 км, поэтому астероид пролетел на расстоянии, равном 10 радиусам Земли. Немного упростим задачу - будем считать, что астероид пересекал прямую, соединяющую наблюдателя и Луну, перпендикулярно. Тогда путь
км, поэтому астероид пролетел на расстоянии, равном 10 радиусам Земли. Немного упростим задачу - будем считать, что астероид пересекал прямую, соединяющую наблюдателя и Луну, перпендикулярно. Тогда путь  , пройденный астероидом на фоне диска Луны, относится к расстоянию до него так же, как диаметр Луны к расстоянию до нее. Отсюда (если выразить все величины в радиусах Земли)
, пройденный астероидом на фоне диска Луны, относится к расстоянию до него так же, как диаметр Луны к расстоянию до нее. Отсюда (если выразить все величины в радиусах Земли) 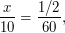 и пройденный путь
и пройденный путь 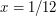 радиуса Земли. Выразив его в километрах, получим,
радиуса Земли. Выразив его в километрах, получим, 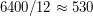 км. Теперь вспомним, что астероид двигался под углом
км. Теперь вспомним, что астероид двигался под углом 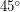 к прямой. Так как расстояние между Землей и Луной намного больше 530 км, то можно считать, что за счет этого путь астероида на фоне диска Луны увеличился в
к прямой. Так как расстояние между Землей и Луной намного больше 530 км, то можно считать, что за счет этого путь астероида на фоне диска Луны увеличился в 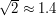 раза. В итоге получаем путь, равный
раза. В итоге получаем путь, равный 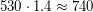 км. Так как астероид двигался со скоростью 20 км/с, время пересечения окажется равным
км. Так как астероид двигался со скоростью 20 км/с, время пересечения окажется равным 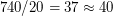 с.
с. - 11 февраля 2009 года на высоте 800~км над поверхностью Земли столкнулись два спутника: "Космос-2251" и "Iridium 33". В момент столкновения угол между траекториями спутников составлял
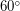 . Найдите диапазон возможных значений относительной скорости спутников при столкновении.
. Найдите диапазон возможных значений относительной скорости спутников при столкновении.
Решение: Спутники столкнулись на сравнительно небольшой высоте. С достаточной точностью можно считать, что в момент столкновения оба спутника находились в перигее (минимально возможная высота полета спутников составляет примерно 300 км, и относительная разница между расстоянием до центра Земли 7200 км и 6700 км невелика). Первая и вторая космические скорости на такой высоте также мало отличаются от <<наземных>> (они пропорциональны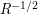 , поэтому отличие не превосходит 6%). Следовательно, минимально возможная скорость каждого спутника около 8 км/с, а максимально возможная - около 11 км/с. Если бы скорости спутников были одинаковыми и равнялись
, поэтому отличие не превосходит 6%). Следовательно, минимально возможная скорость каждого спутника около 8 км/с, а максимально возможная - около 11 км/с. Если бы скорости спутников были одинаковыми и равнялись  , то, так как угол между траекториями составлял
, то, так как угол между траекториями составлял 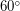 , относительная скорость сближения спутников также равнялась
, относительная скорость сближения спутников также равнялась  . Отсюда очевидно, что возможная относительная скорость спутников заключена в пределах от 8 км/с до 11 км/с.
. Отсюда очевидно, что возможная относительная скорость спутников заключена в пределах от 8 км/с до 11 км/с. - С помощью антенны дальней космической связи, состоящей из нескольких одинаковых рефлекторов (радиотелескопов-"тарелок") выполнялась радиолокация некоторого астероида, движущегося по круговой орбите. Во время противостояния ответный сигнал был принят на пределе чувствительности с использованием двух рефлекторов, а в квадратуре для приема сигнала (также на пределе чувствительности) пришлось задействовать восемь рефлекторов. Мощность излучения локатора в обоих случаях была одинаковой. Найдите радиус орбиты астероида. Какое время прошло между посылкой сигнала и приемом ответного во время сеанса локации в противостоянии?
Решение: Посланный локатором сигнал распространяется в некотором телесном угле, поэтому его интенсивность падает обратно пропорционально квадрату расстояния. Интенсивность излучения, отраженного от астероида, при распространении назад к локатору также уменьшается обратно пропорционально квадрату расстояния, поэтому интенсивность принятого локатором сигнала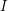 зависит от расстояния до объекта
зависит от расстояния до объекта  как
как 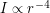 . Из условия ясно, что интенсивность вернувшегося сигнала в противостоянии была в 4 раза больше, чем в квадратуре, следовательно, расстояния до астероида в противостоянии
. Из условия ясно, что интенсивность вернувшегося сигнала в противостоянии была в 4 раза больше, чем в квадратуре, следовательно, расстояния до астероида в противостоянии  и в квадратуре
и в квадратуре  связаны как
связаны как ![$ r_\text{к} = \sqrt[4]{4} r_\text{п} = \sqrt{2} r_\text{п} $](/files/tex/2d895edc6780a92249b414fda36210058c2e94ef.png) Вспомнив определения противостояния (Солнце, Земля и астероид находятся на одной прямой) и квадратуры (направления Солнце-Земля и Земля-астероид образуют прямой угол), можно заметить, что расстояние в противостоянии, выраженное в астрономических единицах, равно
Вспомнив определения противостояния (Солнце, Земля и астероид находятся на одной прямой) и квадратуры (направления Солнце-Земля и Земля-астероид образуют прямой угол), можно заметить, что расстояние в противостоянии, выраженное в астрономических единицах, равно 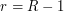 , где
, где 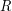 - радиус орбиты астероида (также в а.е.), а расстояние в квадратуре
- радиус орбиты астероида (также в а.е.), а расстояние в квадратуре 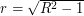 (по теореме Пифагора). Отсюда получаем уравнение
(по теореме Пифагора). Отсюда получаем уравнение 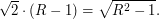 Оно приводится к квадратному
Оно приводится к квадратному 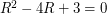 , корни которого равны
, корни которого равны 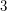 и
и 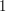 . Корень, равный единице, нас не устраивает по смыслу задачи, поэтому ответ один - радиус орбиты астероида равен 3 а.е.
. Корень, равный единице, нас не устраивает по смыслу задачи, поэтому ответ один - радиус орбиты астероида равен 3 а.е. - Во сколько раз нужно изменить большие полуоси орбит Земли и Луны, чтобы в нашем календаре было 12 месяцев ровно по 30 дней? Настоящий период обращения Луны вокруг Земли -
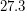 суток.
суток.
Решение: Поскольку продолжительность суток изменять нельзя, то из условия следует, что продолжительность года должна равняться ровно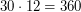 суткам (сейчас она составляет
суткам (сейчас она составляет 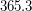 суток). Воспользовавшись III законом Кеплера (
суток). Воспользовавшись III законом Кеплера (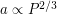 , где
, где  - большая полуось,
- большая полуось, 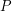 - период), получаем, что большую полуось орбиты Земли надо уменьшить в
- период), получаем, что большую полуось орбиты Земли надо уменьшить в 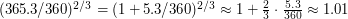 раза. Для решения второй части задачи следует вспомнить, что продолжительность периода повторения фаз Луны - синодический лунный месяц - это не совсем то же самое, что период обращения Луны вокруг Земли. Синодический месяц
раза. Для решения второй части задачи следует вспомнить, что продолжительность периода повторения фаз Луны - синодический лунный месяц - это не совсем то же самое, что период обращения Луны вокруг Земли. Синодический месяц 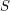 связан с периодом обращения
связан с периодом обращения 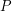 как
как 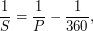 (тут 360 - новая продолжительность года в сутках), отюда желаемый нами период обращения
(тут 360 - новая продолжительность года в сутках), отюда желаемый нами период обращения 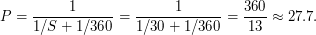 Далее действуем так же, как при решении первой части задачи. В итоге получаем, что большую полуось орбиты Луны надо увеличить в
Далее действуем так же, как при решении первой части задачи. В итоге получаем, что большую полуось орбиты Луны надо увеличить в 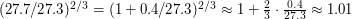 раза.
раза.
Комментарии
6 недель 4 дня назад
6 недель 4 дня назад
7 недель 6 дней назад
10 недель 2 дня назад
10 недель 3 дня назад
13 недель 3 дня назад
13 недель 3 дня назад
18 недель 5 дней назад
18 недель 5 дней назад
22 недели 1 день назад