


Next: Спектры Солнца и звезд
Up: Задачи
Previous: Звездные величины
 8.1
Функция Планка в шкале длин волн имеет вид
8.1
Функция Планка в шкале длин волн имеет вид
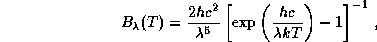
а приближение Вина дается формулой
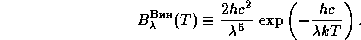
Поэтому
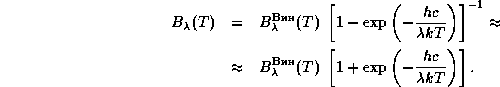
Значит, относительная погрешность приближения Вина 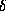 =
=
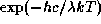 .
С другой стороны, исследуя функцию Вина на максимум, легко найти, что
.
С другой стороны, исследуя функцию Вина на максимум, легко найти, что

Этот очень полезный результат есть закон смещения Вина.
Обычно ограничиваются тем, что отмечают постоянство произведения
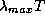 . Однако очень важно и численное значение
. Однако очень важно и численное значение
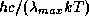 , точнее, то, что это число заметно
превосходит 1. Действительно, мы имеем
, точнее, то, что это число заметно
превосходит 1. Действительно, мы имеем
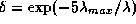 ,
так что
,
так что 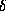 мало при
мало при 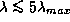 .
Интенсивность в максимуме, которую мы (теперь обоснованно)
вычисляем в приближении Вина, есть
.
Интенсивность в максимуме, которую мы (теперь обоснованно)
вычисляем в приближении Вина, есть
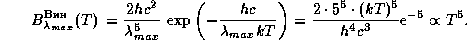
Если не пользоваться приближением Вина, а работать с точной планковской
функцией, то оказывается, что
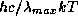 равно не точно 5, а 4.965 (проверьте!).
Все остальное, включая заключение, что
равно не точно 5, а 4.965 (проверьте!).
Все остальное, включая заключение, что
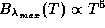 , остается в силе.
, остается в силе.
Длинноволновое приближение Рэлея-Джинса,
противоположное приближению Вина, обеспечивает относительную
погрешность 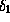 лишь при
лишь при 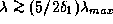 (проверьте).
Скажем, точность в 10% приближение Рэлея-Джинса дает лишь при
(проверьте).
Скажем, точность в 10% приближение Рэлея-Джинса дает лишь при 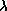 ,
превосходящих
,
превосходящих 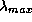 в 25 раз!
в 25 раз!
В итоге оказывается, что вся планковская кривая
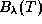 , как ее видит глаз на обычном графике, неотличима от
виновской кривой.
Большинство же студентов (да, пожалуй, и экс-студентов тоже) ошибочно полагает, что
приближение Вина для
, как ее видит глаз на обычном графике, неотличима от
виновской кривой.
Большинство же студентов (да, пожалуй, и экс-студентов тоже) ошибочно полагает, что
приближение Вина для 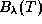 применимо только слева от максимума,
приближение Рэлея-Джинса начинает работать слегка правее него, а сам
максимум хорошо описывается лишь точной формулой Планка. На самом
деле, как мы убедились, все совсем не так.
применимо только слева от максимума,
приближение Рэлея-Джинса начинает работать слегка правее него, а сам
максимум хорошо описывается лишь точной формулой Планка. На самом
деле, как мы убедились, все совсем не так.
 8.2
Планковские кривые, соответствующие разным T, не пересекаются,
поскольку
8.2
Планковские кривые, соответствующие разным T, не пересекаются,
поскольку 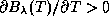 .
Отсюда следует, что при любом (фиксированном)
.
Отсюда следует, что при любом (фиксированном) 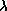 значения
значения 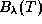 монотонно возрастают с T.
Далее, высота максимума планковской кривой,
т.е. максимальное значение интенсивности,
пропорциональна
монотонно возрастают с T.
Далее, высота максимума планковской кривой,
т.е. максимальное значение интенсивности,
пропорциональна 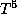 для
для 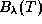 и
и
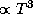 для
для 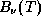 .
Это легко показать, исследуя на максимум соответствующие функции Планка
(см. задачу
.
Это легко показать, исследуя на максимум соответствующие функции Планка
(см. задачу  ).
Площадь же под обеими кривыми, и
).
Площадь же под обеими кривыми, и 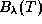 и
и 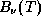 , растет
, растет
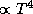 (закон Стефана-Больцмана).
Поэтому с ростом температуры кривая Планка в шкале длин волн
"заостряется", а в шкале частот -- "притупляется".
(закон Стефана-Больцмана).
Поэтому с ростом температуры кривая Планка в шкале длин волн
"заостряется", а в шкале частот -- "притупляется".
 8.3
Пусть f(x) дифференцируема в точке
8.3
Пусть f(x) дифференцируема в точке 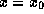 . Для простоты считаем,
что
. Для простоты считаем,
что 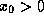 и
и
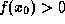 . Для получения степенной аппроксимации f(x) в
окрестности
. Для получения степенной аппроксимации f(x) в
окрестности 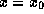 , т.е. представления f(x) вида
, т.е. представления f(x) вида
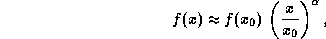
поступим следующим образом. Будем рассматривать 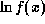 как функцию
как функцию
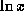 . Тогда имеем обычную линеаризацию в окрестности
. Тогда имеем обычную линеаризацию в окрестности 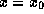 :
:
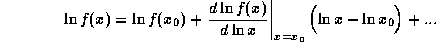
Отсюда, потенцируя, получаем вышеприведенную степенную
аппроксимацию f(x), причем обнаруживается, что
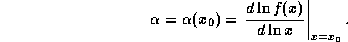
Подобные степенные аппроксимации используются в физике (и, в
частности, в астрофизике) буквально на каждом шагу. К сожалению, ни в
одном известном авторам курсе математического анализа об этом нет ни
слова -- хотя учить этому следовало бы всех, даже изучающих анализ не
слишком глубоко. Видимо, считается, что студент сам все это
сообразит, когда немного "подрастет". Мы решили нарушить традицию
и не ждать, когда это случится.
Приведенная в условии задачи степенная аппроксимация
зависимости чернотельной интенсивности 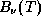 от T в
окрестности
от T в
окрестности 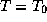 получается только что описанным стандартным способом.
Выкладку предоставляем читателю.
получается только что описанным стандартным способом.
Выкладку предоставляем читателю.
Степенная аппроксимация функции Планка, которую
почему-то не отыщешь ни в одном учебнике, позволяет понять многие
качественные особенности солнечного и звездных спектров. См., в
частности, задачу  .
.
 8.4
А почему, собственно, она должна равняться (3/2)kT? Ведь фотон --
не классическая частица, движущаяся с нерелятивистской скоростью. А
только к таким частицам и применима классическая формула (3/2)kT.
8.4
А почему, собственно, она должна равняться (3/2)kT? Ведь фотон --
не классическая частица, движущаяся с нерелятивистской скоростью. А
только к таким частицам и применима классическая формула (3/2)kT.
Чтобы найти среднюю энергию одного чернотельного фотона
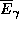 , надо объемную плотность энергии поля излучения
, надо объемную плотность энергии поля излучения
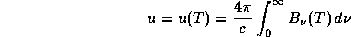
поделить на число фотонов в единице объема
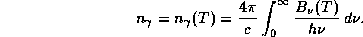
Сделав в обоих интегралах одну и ту же замену
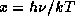 , обнаруживаем, что
, обнаруживаем, что

где
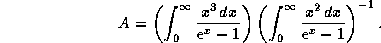
Для оценки A можно воспользоваться приближением Вина, т.е.
пренебречь 1 по сравнению с 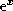 в двух последних интегралах
(ср. с обсуждением в задаче
в двух последних интегралах
(ср. с обсуждением в задаче  ). Тогда немедленно получим,
что
). Тогда немедленно получим,
что
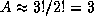 , поскольку (советуем это запомнить)
, поскольку (советуем это запомнить)
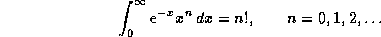
Последнее легко доказывается интегрированием по частям. Итак,
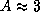 ; вычислив интегралы точно, мы нашли бы, что A=2.70, так
что окончательно
; вычислив интегралы точно, мы нашли бы, что A=2.70, так
что окончательно

Таким образом, средняя энергия одного чернотельного фотона без малого
вдвое больше средней энергии теплового движения нерелятивистской частицы.
Однако вклад
каждого фотона в давление почти в точности такой же, как и каждой
частицы: давление излучения 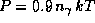 ,
газовое же давление P = n k T,
где
,
газовое же давление P = n k T,
где 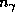 и n -- концентрации фотонов и частиц, соответственно.
(Как вы думаете, почему так получается? Впрочем, это уже скорее
физика, чем астрономия. Но ведь решаемся же мы нет-нет да
и приучить вас к "физической математике", так почему же не поучить
чуть-чуть и "астрономической физике"?)
Из только что сказанного следует, что отношение концентраций фотонов
и частиц есть одновременно (с точностью
и n -- концентрации фотонов и частиц, соответственно.
(Как вы думаете, почему так получается? Впрочем, это уже скорее
физика, чем астрономия. Но ведь решаемся же мы нет-нет да
и приучить вас к "физической математике", так почему же не поучить
чуть-чуть и "астрономической физике"?)
Из только что сказанного следует, что отношение концентраций фотонов
и частиц есть одновременно (с точностью 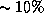 ) и отношение
давления излучения к газовому (см. задачу
) и отношение
давления излучения к газовому (см. задачу  ).
).
 8.5
Выражение для
8.5
Выражение для 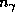 уже появлялось в решении предыдущей задачи:
уже появлялось в решении предыдущей задачи:
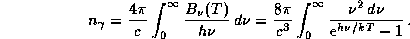
Подстановка 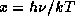 приводит его к виду
приводит его к виду
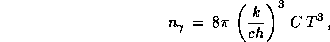
где

Таким образом, 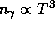 .
Чтобы найти точное значение коэффициента пропорциональности,
надо получить C.
Как мы знаем (см. решение предыдущей задачи),
приближенно можно считать, что C=2.
Точное же значение C получается так:
.
Чтобы найти точное значение коэффициента пропорциональности,
надо получить C.
Как мы знаем (см. решение предыдущей задачи),
приближенно можно считать, что C=2.
Точное же значение C получается так:
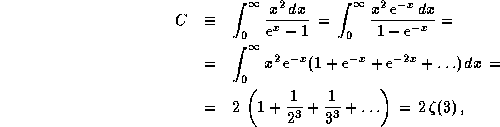
где 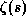 -- дзета-функция Римана:
-- дзета-функция Римана:
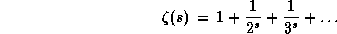
Число 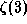 не выражается через какие-либо "стандартные"
постоянные (
не выражается через какие-либо "стандартные"
постоянные ( , e, постоянную Эйлера и т.п.).
Оно равно
, e, постоянную Эйлера и т.п.).
Оно равно 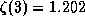 .
.
После подстановки всех постоянных в полученное выше выражение для
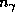 находим, что
находим, что

Мы несколько отступили здесь от нашего обычного стиля --
получать скорее оценки, чем точные результаты, и стараться избегать
громоздких расчетов.
Сделать это хотя бы один раз, однако, полезно.
А вот как формулу 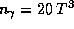 можно получить совсем просто,
комбинируя другие известные результаты.
Плотность лучистой энергии равновесного излучения равна
можно получить совсем просто,
комбинируя другие известные результаты.
Плотность лучистой энергии равновесного излучения равна

где a -- постоянная плотности излучения:
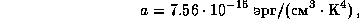
а средняя энергия одного фотона
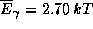 (см. предыдущую задачу).
Поэтому
(см. предыдущую задачу).
Поэтому
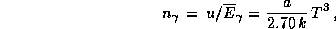
что сразу же и дает коэффициент 20 при 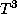 .
На самом деле, конечно, ничего принципиально нового в таком
способе расчета нет -- просто мы
использовали готовое численное значение постоянной плотности излучения a
(оно есть, например, у Аллена [1]).
.
На самом деле, конечно, ничего принципиально нового в таком
способе расчета нет -- просто мы
использовали готовое численное значение постоянной плотности излучения a
(оно есть, например, у Аллена [1]).
 8.6
Частота фотона, испускаемого при переходе атома водорода с уровня m на
уровень n, дается известной формулой
8.6
Частота фотона, испускаемого при переходе атома водорода с уровня m на
уровень n, дается известной формулой
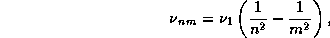
где 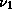 -- частота предела ионизации с первого уровня,
-- частота предела ионизации с первого уровня,
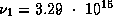 Гц.
Гц.
Перейдем от частот к длинам волн:

где 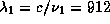
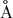 .
.
Искомый переход найдем перебором. Вначале положим n=1.
Тогда для m=2 получаем 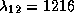
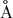 .
Это знаменитая линия лайман-альфа, или
.
Это знаменитая линия лайман-альфа, или 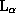 .
Ясно, что для m>2 будем иметь
.
Ясно, что для m>2 будем иметь 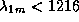
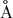 , т.е.
переходы на первый уровень нам не подходят.
Возьмем n=2.
Тогда для m=3 получим
, т.е.
переходы на первый уровень нам не подходят.
Возьмем n=2.
Тогда для m=3 получим 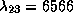
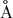 .
Это и есть искомый переход (линия H
.
Это и есть искомый переход (линия H ).
Различие в длине волны в четвертом знаке (6 вместо 3) нас смущать не должно,
так как при расчете мы использовали значение
).
Различие в длине волны в четвертом знаке (6 вместо 3) нас смущать не должно,
так как при расчете мы использовали значение 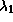 лишь
с тремя значащими цифрами.
лишь
с тремя значащими цифрами.
 8.7
По формуле из решения предыдущей задачи находим
8.7
По формуле из решения предыдущей задачи находим
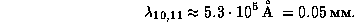
Таким образом, линия межзвездного водорода H 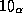 лежит в
субмиллиметровом диапазоне.
Излучение в нем поглощается земной атмосферой.
Наземные наблюдения линии невозможны.
лежит в
субмиллиметровом диапазоне.
Излучение в нем поглощается земной атмосферой.
Наземные наблюдения линии невозможны.
 8.8
Линия H
8.8
Линия H 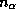 возникает при переходе
возникает при переходе 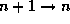 в атоме водорода.
Из общей сериальной формулы для водорода (см. задачу
в атоме водорода.
Из общей сериальной формулы для водорода (см. задачу  )
)

полагая m=n+1 и считая, что 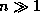 , находим
, находим
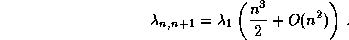
Согласно этой формуле, линия H 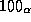 , например, имеет
длину волны около 5 см.
, например, имеет
длину волны около 5 см.
Подобные радиолинии, возникающие при переходах между близкими
высокорасположенными уровнями, давно уже наблюдаются в туманностях.
Как вы думаете, есть ли надежда обнаружить их также в
радиоизлучении Солнца? (Ср. задачу  .)
.)
 8.9
Исходим из сериальной формулы для водорода в шкале частот:
8.9
Исходим из сериальной формулы для водорода в шкале частот:
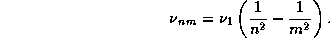
Полагая в ней 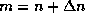 и считая, что
и считая, что 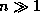 и
и 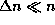 ,
получим
,
получим
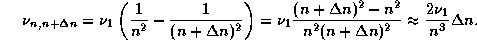
Отсюда видно, что, действительно, при увеличении 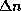 на единицу частота соответствующего перехода
возрастает на одну и ту же величину
на единицу частота соответствующего перехода
возрастает на одну и ту же величину
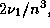 которая есть не что иное как частота линии H
которая есть не что иное как частота линии H 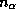 .
.
 8.10
Ионизация атомов водорода с n-го уровня может производиться
фотонами с длиной волны короче, чем та, которую имеет излучение, образующееся
при переходе атома водорода с уровня
8.10
Ионизация атомов водорода с n-го уровня может производиться
фотонами с длиной волны короче, чем та, которую имеет излучение, образующееся
при переходе атома водорода с уровня  на уровень n.
По формуле из решения задачи
на уровень n.
По формуле из решения задачи  находим, что эта длина волны равна
находим, что эта длина волны равна
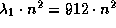
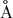 .
При n = 2 имеем 3648
.
При n = 2 имеем 3648 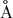 (на самом деле 3646
(на самом деле 3646 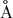 ).
Таким образом, излучение видимого диапазона не способно ионизовать
атомы водорода со второго уровня. Это очень важное заключение.
).
Таким образом, излучение видимого диапазона не способно ионизовать
атомы водорода со второго уровня. Это очень важное заключение.
 8.11
Причина этого -- различие плотности. В
атмосферах белых карликов она значительно выше, чем в солнечной
хромосфере (почему?). Поэтому средние расстояния между атомами
в хромосфере гораздо больше, чем в атмосферах белых карликов.
Но радиус n-й боровской орбиты
8.11
Причина этого -- различие плотности. В
атмосферах белых карликов она значительно выше, чем в солнечной
хромосфере (почему?). Поэтому средние расстояния между атомами
в хромосфере гораздо больше, чем в атмосферах белых карликов.
Но радиус n-й боровской орбиты 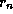 быстро растет с n, именно,
быстро растет с n, именно,
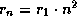 . Понятно, что он не может быть больше среднего
расстояния между атомами -- иначе станет непонятно, какому именно
атому принадлежит электрон, находящийся на этом уровне, т.е.
произойдет его "обобществление". Поэтому, чем выше плотность, тем
меньшее число уровней реализуется, а потому и тем меньшее число
бальмеровских линий может возникать.
. Понятно, что он не может быть больше среднего
расстояния между атомами -- иначе станет непонятно, какому именно
атому принадлежит электрон, находящийся на этом уровне, т.е.
произойдет его "обобществление". Поэтому, чем выше плотность, тем
меньшее число уровней реализуется, а потому и тем меньшее число
бальмеровских линий может возникать.
Удивительно, но факт: просто подсчитывая число бальмеровских линий,
которые видны в спектре той или иной звезды, можно оценить
плотность ее атмосферы!
©
В.В.Иванов,
А.В.Кривов,
П.А.Денисенков
HTML by Igor Drozdovsky
Последнее обновление:



Next: Спектры Солнца и звезд
Up: Задачи
Previous: Звездные величины

 8.1
Функция Планка в шкале длин волн имеет вид
8.1
Функция Планка в шкале длин волн имеет вид
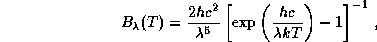
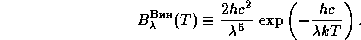
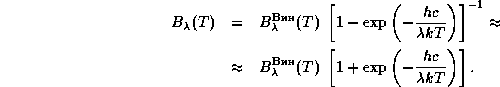
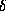 =
=
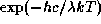 .
С другой стороны, исследуя функцию Вина на максимум, легко найти, что
.
С другой стороны, исследуя функцию Вина на максимум, легко найти, что

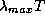 . Однако очень важно и численное значение
. Однако очень важно и численное значение
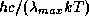 , точнее, то, что это число заметно
превосходит 1. Действительно, мы имеем
, точнее, то, что это число заметно
превосходит 1. Действительно, мы имеем
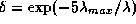 ,
так что
,
так что 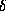 мало при
мало при 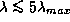 .
Интенсивность в максимуме, которую мы (теперь обоснованно)
вычисляем в приближении Вина, есть
.
Интенсивность в максимуме, которую мы (теперь обоснованно)
вычисляем в приближении Вина, есть
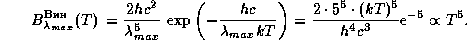



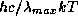 равно не точно 5, а 4.965 (проверьте!).
Все остальное, включая заключение, что
равно не точно 5, а 4.965 (проверьте!).
Все остальное, включая заключение, что
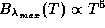 , остается в силе.
, остается в силе.
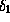 лишь при
лишь при 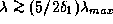 (проверьте).
Скажем, точность в 10% приближение Рэлея-Джинса дает лишь при
(проверьте).
Скажем, точность в 10% приближение Рэлея-Джинса дает лишь при 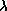 ,
превосходящих
,
превосходящих 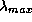 в 25 раз!
в 25 раз!
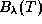 , как ее видит глаз на обычном графике, неотличима от
виновской кривой.
Большинство же студентов (да, пожалуй, и экс-студентов тоже) ошибочно полагает, что
приближение Вина для
, как ее видит глаз на обычном графике, неотличима от
виновской кривой.
Большинство же студентов (да, пожалуй, и экс-студентов тоже) ошибочно полагает, что
приближение Вина для 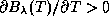 .
Отсюда следует, что при любом (фиксированном)
.
Отсюда следует, что при любом (фиксированном) 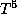 для
для 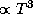 для
для 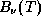 .
Это легко показать, исследуя на максимум соответствующие функции Планка
(см. задачу
.
Это легко показать, исследуя на максимум соответствующие функции Планка
(см. задачу 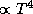 (закон Стефана-Больцмана).
Поэтому с ростом температуры кривая Планка в шкале длин волн
"заостряется", а в шкале частот -- "притупляется".
(закон Стефана-Больцмана).
Поэтому с ростом температуры кривая Планка в шкале длин волн
"заостряется", а в шкале частот -- "притупляется".
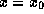 . Для простоты считаем,
что
. Для простоты считаем,
что 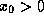 и
и
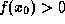 . Для получения степенной аппроксимации f(x) в
окрестности
. Для получения степенной аппроксимации f(x) в
окрестности 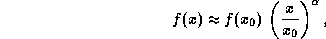
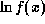 как функцию
как функцию
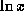 . Тогда имеем обычную линеаризацию в окрестности
. Тогда имеем обычную линеаризацию в окрестности 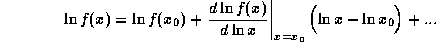
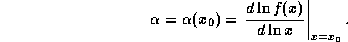
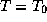 получается только что описанным стандартным способом.
Выкладку предоставляем читателю.
получается только что описанным стандартным способом.
Выкладку предоставляем читателю.
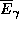 , надо объемную плотность энергии поля излучения
, надо объемную плотность энергии поля излучения
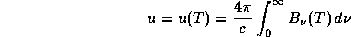
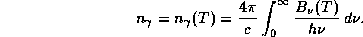
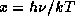 , обнаруживаем, что
, обнаруживаем, что

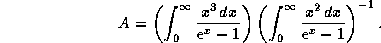
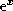 в двух последних интегралах
(ср. с обсуждением в задаче
в двух последних интегралах
(ср. с обсуждением в задаче 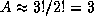 , поскольку (советуем это запомнить)
, поскольку (советуем это запомнить)
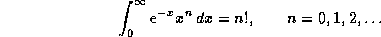
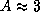 ; вычислив интегралы точно, мы нашли бы, что A=2.70, так
что окончательно
; вычислив интегралы точно, мы нашли бы, что A=2.70, так
что окончательно

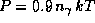 ,
газовое же давление P = n k T,
где
,
газовое же давление P = n k T,
где 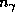 и n -- концентрации фотонов и частиц, соответственно.
(Как вы думаете, почему так получается? Впрочем, это уже скорее
физика, чем астрономия. Но ведь решаемся же мы нет-нет да
и приучить вас к "физической математике", так почему же не поучить
чуть-чуть и "астрономической физике"?)
Из только что сказанного следует, что отношение концентраций фотонов
и частиц есть одновременно (с точностью
и n -- концентрации фотонов и частиц, соответственно.
(Как вы думаете, почему так получается? Впрочем, это уже скорее
физика, чем астрономия. Но ведь решаемся же мы нет-нет да
и приучить вас к "физической математике", так почему же не поучить
чуть-чуть и "астрономической физике"?)
Из только что сказанного следует, что отношение концентраций фотонов
и частиц есть одновременно (с точностью 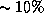 ) и отношение
давления излучения к газовому (см. задачу
) и отношение
давления излучения к газовому (см. задачу 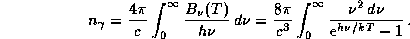
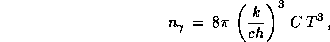

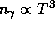 .
Чтобы найти точное значение коэффициента пропорциональности,
надо получить C.
Как мы знаем (см. решение предыдущей задачи),
приближенно можно считать, что C=2.
Точное же значение C получается так:
.
Чтобы найти точное значение коэффициента пропорциональности,
надо получить C.
Как мы знаем (см. решение предыдущей задачи),
приближенно можно считать, что C=2.
Точное же значение C получается так:
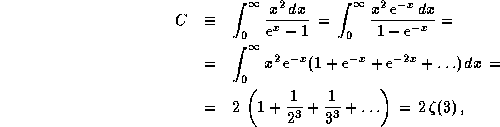
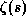 -- дзета-функция Римана:
-- дзета-функция Римана:
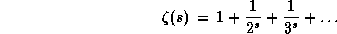
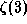 не выражается через какие-либо "стандартные"
постоянные (
не выражается через какие-либо "стандартные"
постоянные ( , e, постоянную Эйлера и т.п.).
Оно равно
, e, постоянную Эйлера и т.п.).
Оно равно 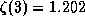 .
.

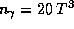 можно получить совсем просто,
комбинируя другие известные результаты.
Плотность лучистой энергии равновесного излучения равна
можно получить совсем просто,
комбинируя другие известные результаты.
Плотность лучистой энергии равновесного излучения равна

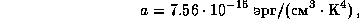
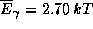 (см. предыдущую задачу).
Поэтому
(см. предыдущую задачу).
Поэтому
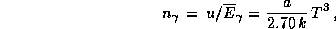
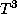 .
На самом деле, конечно, ничего принципиально нового в таком
способе расчета нет -- просто мы
использовали готовое численное значение постоянной плотности излучения a
(оно есть, например, у Аллена
.
На самом деле, конечно, ничего принципиально нового в таком
способе расчета нет -- просто мы
использовали готовое численное значение постоянной плотности излучения a
(оно есть, например, у Аллена 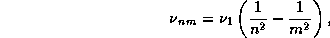
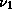 -- частота предела ионизации с первого уровня,
-- частота предела ионизации с первого уровня,
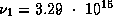 Гц.
Гц.

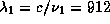
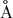 .
.
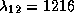
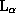 .
Ясно, что для m>2 будем иметь
.
Ясно, что для m>2 будем иметь 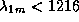
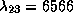
 ).
Различие в длине волны в четвертом знаке (6 вместо 3) нас смущать не должно,
так как при расчете мы использовали значение
).
Различие в длине волны в четвертом знаке (6 вместо 3) нас смущать не должно,
так как при расчете мы использовали значение 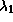 лишь
с тремя значащими цифрами.
лишь
с тремя значащими цифрами.
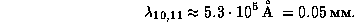
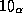 лежит в
субмиллиметровом диапазоне.
Излучение в нем поглощается земной атмосферой.
Наземные наблюдения линии невозможны.
лежит в
субмиллиметровом диапазоне.
Излучение в нем поглощается земной атмосферой.
Наземные наблюдения линии невозможны.
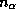 возникает при переходе
возникает при переходе 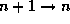 в атоме водорода.
Из общей сериальной формулы для водорода (см. задачу
в атоме водорода.
Из общей сериальной формулы для водорода (см. задачу 
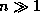 , находим
, находим
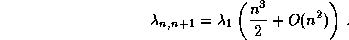
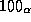 , например, имеет
длину волны около 5 см.
, например, имеет
длину волны около 5 см.
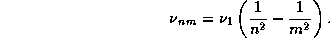
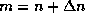 и считая, что
и считая, что 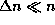 ,
получим
,
получим
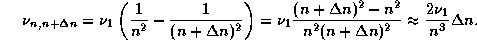
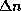 на единицу частота соответствующего перехода
возрастает на одну и ту же величину
на единицу частота соответствующего перехода
возрастает на одну и ту же величину
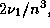 которая есть не что иное как частота линии H
которая есть не что иное как частота линии H  на уровень n.
По формуле из решения задачи
на уровень n.
По формуле из решения задачи 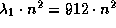
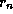 быстро растет с n, именно,
быстро растет с n, именно,
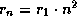 . Понятно, что он не может быть больше среднего
расстояния между атомами -- иначе станет непонятно, какому именно
атому принадлежит электрон, находящийся на этом уровне, т.е.
произойдет его "обобществление". Поэтому, чем выше плотность, тем
меньшее число уровней реализуется, а потому и тем меньшее число
бальмеровских линий может возникать.
. Понятно, что он не может быть больше среднего
расстояния между атомами -- иначе станет непонятно, какому именно
атому принадлежит электрон, находящийся на этом уровне, т.е.
произойдет его "обобществление". Поэтому, чем выше плотность, тем
меньшее число уровней реализуется, а потому и тем меньшее число
бальмеровских линий может возникать.