


Next: Галактика
Up: Задачи
Previous: Двойные и переменные звезды
Решения
 14.1
Межзвездное поглощение
14.1
Межзвездное поглощение 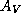 в полосе V связано с избытком цвета
в полосе V связано с избытком цвета
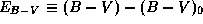 известным соотношением
известным соотношением

По условию задачи 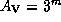 . Далее,
истинный показатель цвета
. Далее,
истинный показатель цвета 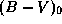 у звезды
класса A0 равен нулю по определению показателя цвета.
Поэтому искомый наблюдаемый показатель цвета равен
у звезды
класса A0 равен нулю по определению показателя цвета.
Поэтому искомый наблюдаемый показатель цвета равен
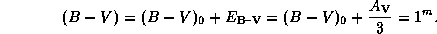
 14.2
Поглощаемое туманностью излучение центральной звезды -- это
излучение в далеком ультрафиолете
(лаймановский континуум,
14.2
Поглощаемое туманностью излучение центральной звезды -- это
излучение в далеком ультрафиолете
(лаймановский континуум, 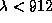
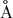 ). При столь высокой
температуре звезды большая часть ее излучения приходится на
лаймановский континуум, и потому поглощается туманностью,
ионизуя водород.
В видимой же области
спектра туманность прозрачна и для излучения центральной звезды, и для
излучения просвечивающих сквозь нее далеких объектов.
). При столь высокой
температуре звезды большая часть ее излучения приходится на
лаймановский континуум, и потому поглощается туманностью,
ионизуя водород.
В видимой же области
спектра туманность прозрачна и для излучения центральной звезды, и для
излучения просвечивающих сквозь нее далеких объектов.
 14.3
Число фотонов, испускаемое за единицу времени с 1 см2 черного тела
температуры T, равно
14.3
Число фотонов, испускаемое за единицу времени с 1 см2 черного тела
температуры T, равно 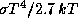 .
Здесь
.
Здесь 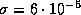 --
постоянная Стефана, а
--
постоянная Стефана, а 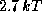 -- это средняя энергия одного
чернотельного фотона (см. задачу
-- это средняя энергия одного
чернотельного фотона (см. задачу  ).
Так как температура звезды по условию задачи очень высока, почти все
эти фотоны принадлежат лаймановскому континууму (
).
Так как температура звезды по условию задачи очень высока, почти все
эти фотоны принадлежат лаймановскому континууму (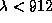
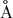 )
и, значит, почти каждый из них может ионизовать атом водорода.
Поэтому полное число ионизаций за 1 с близко к полному числу фотонов,
излучаемых звездой за единицу времени:
)
и, значит, почти каждый из них может ионизовать атом водорода.
Поэтому полное число ионизаций за 1 с близко к полному числу фотонов,
излучаемых звездой за единицу времени:
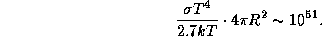
Чтобы облегчить вычисления,
температура звезды, заданная в условии задачи, несколько завышена по
сравнению с теми температурами, которые обычно имеют звезды,
возбуждающие свечение газовых туманностей. Звезда класса O5 имеет
температуру около 50000 K и испускает ежесекундно 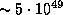 лаймановских фотонов. Это неплохо согласуется с нашей
оценкой, если учесть, что двукратное различие в температуре дает
различие в числе фотонов в 8 раз.
лаймановских фотонов. Это неплохо согласуется с нашей
оценкой, если учесть, что двукратное различие в температуре дает
различие в числе фотонов в 8 раз.
 14.4
Ионизовать водород способно лишь излучение с длиной волны
14.4
Ионизовать водород способно лишь излучение с длиной волны
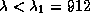
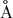 , или с частотой
, или с частотой
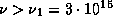 с
с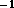 .
Если считать, что спектр излучения звезды
чернотельный, то искомая доля энергии равна
.
Если считать, что спектр излучения звезды
чернотельный, то искомая доля энергии равна
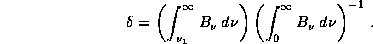
При 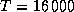 K для получения хорошей оценки величины
K для получения хорошей оценки величины 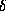 функцию Планка можно брать в приближении Вина:
функцию Планка можно брать в приближении Вина:
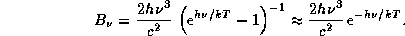
(Обосновать последнее утверждение, пользуясь решением задачи  ).
).
В первоначальной версии рукописи здесь стояло: "В результате
несложных вычислений находим 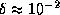 ". Однако один из
авторов настоял, что нужно
воспользоваться этим случаем, чтобы проиллюстрировать, как
грамотно вести оценочные расчеты.
". Однако один из
авторов настоял, что нужно
воспользоваться этим случаем, чтобы проиллюстрировать, как
грамотно вести оценочные расчеты.
Введем безразмерную частоту 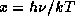 . Для водорода
. Для водорода
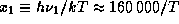 . Появившийся здесь коэффициент
160000 -- это энергия ионизации водорода (13.6 эВ) в
температурной шкале. Это число очень полезно помнить. Оно часто
появляется в самых разных астрофизических задачах. При
. Появившийся здесь коэффициент
160000 -- это энергия ионизации водорода (13.6 эВ) в
температурной шкале. Это число очень полезно помнить. Оно часто
появляется в самых разных астрофизических задачах. При
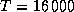 K, заданных в условии задачи, мы
имеем поэтому
K, заданных в условии задачи, мы
имеем поэтому 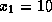 , так что
, так что
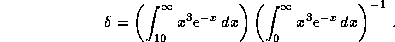
Ясно, что при  экспонента меняется гораздо быстрее, чем
экспонента меняется гораздо быстрее, чем 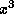 ,
и поэтому
,
и поэтому
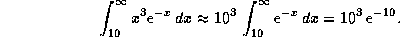
Это вполне приличная оценка (погрешность 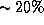 ). Ее можно
уточнять, интегрируя несколько раз по частям и получая каждый раз все более
точные результаты, но нам это вряд ли потребуется.
Далее (см. задачу
). Ее можно
уточнять, интегрируя несколько раз по частям и получая каждый раз все более
точные результаты, но нам это вряд ли потребуется.
Далее (см. задачу  ),
),
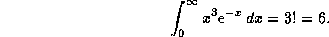
Итак,

Советуем запомнить, что с очень хорошей точностью  (на
самом деле
(на
самом деле 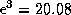 ) -- это часто помогает делать быстрые
оценки. Поэтому
) -- это часто помогает делать быстрые
оценки. Поэтому 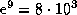 , и мы получаем
, и мы получаем
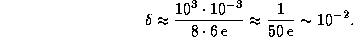
Учить такой кухне прикидочных расчетов почему-то
считается почти что неприличным -- а в результате
студенты зря теряют массу времени попусту.
 14.5
Основная составляющая газовых туманностей и межзвездной среды -- это
водород.
В областях HII он практически полностью ионизован (отсюда и
их название).
Поэтому
14.5
Основная составляющая газовых туманностей и межзвездной среды -- это
водород.
В областях HII он практически полностью ионизован (отсюда и
их название).
Поэтому 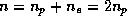 , где
, где 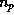 и
и 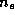 --
концентрации протонов и электронов, соответственно.
Полное число
ионизаций во всей области HII за единицу времени равно полному числу
ионизующих фотонов, испускаемых возбуждающей звездой и поглощаемых в
области HII.
Оно, очевидно, не зависит от концентрации частиц в самой области HII.
В стационарном состоянии
полное число ионизаций должно равняться полному числу рекомбинаций.
Рекомбинации происходят при столкновениях протонов и электронов, и
потому число их в единице объема пропорционально
--
концентрации протонов и электронов, соответственно.
Полное число
ионизаций во всей области HII за единицу времени равно полному числу
ионизующих фотонов, испускаемых возбуждающей звездой и поглощаемых в
области HII.
Оно, очевидно, не зависит от концентрации частиц в самой области HII.
В стационарном состоянии
полное число ионизаций должно равняться полному числу рекомбинаций.
Рекомбинации происходят при столкновениях протонов и электронов, и
потому число их в единице объема пропорционально 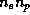 , или
, или
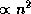 . Поэтому полное число рекомбинаций во всей области HII
пропорционально
. Поэтому полное число рекомбинаций во всей области HII
пропорционально 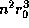 , где
, где 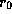 -- радиус области HII.
С другой стороны, оно равно числу ионизаций -- фиксированному числу,
определяемому параметрами возбуждающей звезды (ее радиусом и
температурой). Итак,
-- радиус области HII.
С другой стороны, оно равно числу ионизаций -- фиксированному числу,
определяемому параметрами возбуждающей звезды (ее радиусом и
температурой). Итак, 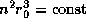 , откуда и следует, что
, откуда и следует, что
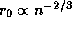 .
.
 14.6
Масса молекулы водорода H2 примерно равна удвоенной массе протона,
т.е.
14.6
Масса молекулы водорода H2 примерно равна удвоенной массе протона,
т.е. 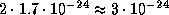 г.
Объем облака по порядку величины есть
г.
Объем облака по порядку величины есть
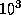 пк
пк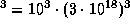 см
см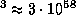 см3.
Поэтому масса облака составляет
см3.
Поэтому масса облака составляет
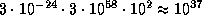 г
г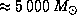 .
.
 14.7
Проходящее сквозь газ излучение ослабляется в e
14.7
Проходящее сквозь газ излучение ослабляется в e раз,
где
раз,
где  -- оптическая толщина слоя газа.
В центре линии L
-- оптическая толщина слоя газа.
В центре линии L она равна
она равна 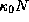 ,
где N -- полное число атомов водорода на луче зрения.
Будем считать, что поглощение становится заметным, когда
,
где N -- полное число атомов водорода на луче зрения.
Будем считать, что поглощение становится заметным, когда 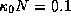 .
Соответствующая масса на луче зрения составляет
.
Соответствующая масса на луче зрения составляет
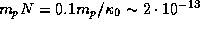 г/см2.
Ошеломляющий результат, не правда ли?
Вывод: спектральный анализ обладает колоссальной чувствительностью.
Он позволяет выявлять присутствие совершенно ничтожных количеств вещества.
г/см2.
Ошеломляющий результат, не правда ли?
Вывод: спектральный анализ обладает колоссальной чувствительностью.
Он позволяет выявлять присутствие совершенно ничтожных количеств вещества.
©
В.В.Иванов,
А.В.Кривов,
П.А.Денисенков
HTML by Igor Drozdovsky
Последнее обновление:



Next: Галактика
Up: Задачи
Previous: Двойные и переменные звезды

 14.1
Межзвездное поглощение
14.1
Межзвездное поглощение 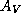 в полосе V связано с избытком цвета
в полосе V связано с избытком цвета
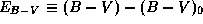 известным соотношением
известным соотношением

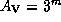 . Далее,
истинный показатель цвета
. Далее,
истинный показатель цвета 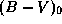 у звезды
класса A0 равен нулю по определению показателя цвета.
Поэтому искомый наблюдаемый показатель цвета равен
у звезды
класса A0 равен нулю по определению показателя цвета.
Поэтому искомый наблюдаемый показатель цвета равен
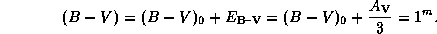



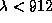
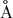 ). При столь высокой
температуре звезды большая часть ее излучения приходится на
лаймановский континуум, и потому поглощается туманностью,
ионизуя водород.
В видимой же области
спектра туманность прозрачна и для излучения центральной звезды, и для
излучения просвечивающих сквозь нее далеких объектов.
). При столь высокой
температуре звезды большая часть ее излучения приходится на
лаймановский континуум, и потому поглощается туманностью,
ионизуя водород.
В видимой же области
спектра туманность прозрачна и для излучения центральной звезды, и для
излучения просвечивающих сквозь нее далеких объектов.
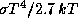 .
Здесь
.
Здесь 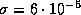 --
постоянная Стефана, а
--
постоянная Стефана, а 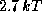 -- это средняя энергия одного
чернотельного фотона (см. задачу
-- это средняя энергия одного
чернотельного фотона (см. задачу 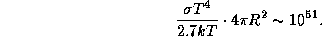
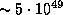 лаймановских фотонов. Это неплохо согласуется с нашей
оценкой, если учесть, что двукратное различие в температуре дает
различие в числе фотонов в 8 раз.
лаймановских фотонов. Это неплохо согласуется с нашей
оценкой, если учесть, что двукратное различие в температуре дает
различие в числе фотонов в 8 раз.
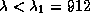
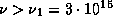 с
с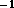 .
Если считать, что спектр излучения звезды
чернотельный, то искомая доля энергии равна
.
Если считать, что спектр излучения звезды
чернотельный, то искомая доля энергии равна
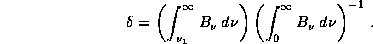
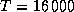 K для получения хорошей оценки величины
K для получения хорошей оценки величины 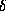 функцию Планка можно брать в приближении Вина:
функцию Планка можно брать в приближении Вина:
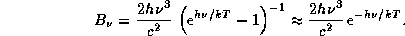
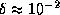 ". Однако один из
авторов настоял, что нужно
воспользоваться этим случаем, чтобы проиллюстрировать, как
грамотно вести оценочные расчеты.
". Однако один из
авторов настоял, что нужно
воспользоваться этим случаем, чтобы проиллюстрировать, как
грамотно вести оценочные расчеты.
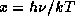 . Для водорода
. Для водорода
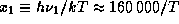 . Появившийся здесь коэффициент
160000 -- это энергия ионизации водорода (13.6 эВ) в
температурной шкале. Это число очень полезно помнить. Оно часто
появляется в самых разных астрофизических задачах. При
. Появившийся здесь коэффициент
160000 -- это энергия ионизации водорода (13.6 эВ) в
температурной шкале. Это число очень полезно помнить. Оно часто
появляется в самых разных астрофизических задачах. При
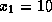 , так что
, так что
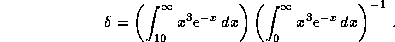
 экспонента меняется гораздо быстрее, чем
экспонента меняется гораздо быстрее, чем 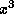 ,
и поэтому
,
и поэтому
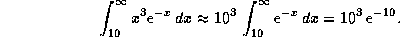
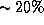 ). Ее можно
уточнять, интегрируя несколько раз по частям и получая каждый раз все более
точные результаты, но нам это вряд ли потребуется.
Далее (см. задачу
). Ее можно
уточнять, интегрируя несколько раз по частям и получая каждый раз все более
точные результаты, но нам это вряд ли потребуется.
Далее (см. задачу 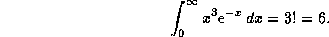

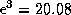 ) -- это часто помогает делать быстрые
оценки. Поэтому
) -- это часто помогает делать быстрые
оценки. Поэтому 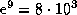 , и мы получаем
, и мы получаем
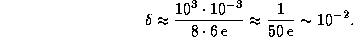
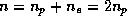 , где
, где 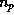 и
и 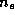 --
концентрации протонов и электронов, соответственно.
Полное число
ионизаций во всей области HII за единицу времени равно полному числу
ионизующих фотонов, испускаемых возбуждающей звездой и поглощаемых в
области HII.
Оно, очевидно, не зависит от концентрации частиц в самой области HII.
В стационарном состоянии
полное число ионизаций должно равняться полному числу рекомбинаций.
Рекомбинации происходят при столкновениях протонов и электронов, и
потому число их в единице объема пропорционально
--
концентрации протонов и электронов, соответственно.
Полное число
ионизаций во всей области HII за единицу времени равно полному числу
ионизующих фотонов, испускаемых возбуждающей звездой и поглощаемых в
области HII.
Оно, очевидно, не зависит от концентрации частиц в самой области HII.
В стационарном состоянии
полное число ионизаций должно равняться полному числу рекомбинаций.
Рекомбинации происходят при столкновениях протонов и электронов, и
потому число их в единице объема пропорционально 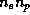 , или
, или
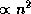 . Поэтому полное число рекомбинаций во всей области HII
пропорционально
. Поэтому полное число рекомбинаций во всей области HII
пропорционально 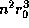 , где
, где 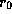 -- радиус области HII.
С другой стороны, оно равно числу ионизаций -- фиксированному числу,
определяемому параметрами возбуждающей звезды (ее радиусом и
температурой). Итак,
-- радиус области HII.
С другой стороны, оно равно числу ионизаций -- фиксированному числу,
определяемому параметрами возбуждающей звезды (ее радиусом и
температурой). Итак, 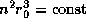 , откуда и следует, что
, откуда и следует, что
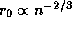 .
.
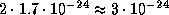 г.
Объем облака по порядку величины есть
г.
Объем облака по порядку величины есть
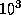 пк
пк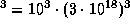 см
см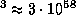 см3.
Поэтому масса облака составляет
см3.
Поэтому масса облака составляет
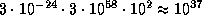 г
г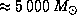 .
.
 раз,
где
раз,
где  -- оптическая толщина слоя газа.
В центре линии L
-- оптическая толщина слоя газа.
В центре линии L она равна
она равна 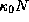 ,
где N -- полное число атомов водорода на луче зрения.
Будем считать, что поглощение становится заметным, когда
,
где N -- полное число атомов водорода на луче зрения.
Будем считать, что поглощение становится заметным, когда 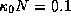 .
Соответствующая масса на луче зрения составляет
.
Соответствующая масса на луче зрения составляет
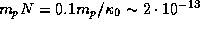 г/см2.
Ошеломляющий результат, не правда ли?
Вывод: спектральный анализ обладает колоссальной чувствительностью.
Он позволяет выявлять присутствие совершенно ничтожных количеств вещества.
г/см2.
Ошеломляющий результат, не правда ли?
Вывод: спектральный анализ обладает колоссальной чувствительностью.
Он позволяет выявлять присутствие совершенно ничтожных количеств вещества.