 13.1
Первая величина есть лучевая скорость центра масс двойной.
13.1
Первая величина есть лучевая скорость центра масс двойной.



13. Двойные и переменные звезды
 13.1
Первая величина есть лучевая скорость центра масс двойной.
13.1
Первая величина есть лучевая скорость центра масс двойной.
Вычислим второй интеграл.
Если центр масс двойной покоится,
то для лучевой скорости нетрудно получить формулу
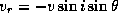 , где v -- орбитальная скорость,
i -- угол между лучом зрения и нормалью к орбите,
а
, где v -- орбитальная скорость,
i -- угол между лучом зрения и нормалью к орбите,
а 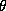 -- полярный угол в плоскости орбиты, за один оборот
пробегающий значения от 0 до
-- полярный угол в плоскости орбиты, за один оборот
пробегающий значения от 0 до 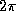 , так что
, так что 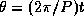 .
Имеем
.
Имеем
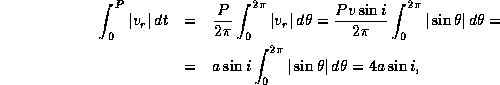
где a -- радиус орбиты.
 13.2
По периоду изменения блеска
13.2
По периоду изменения блеска  Cep оценим ее
среднюю абсолютную звездную величину:
Cep оценим ее
среднюю абсолютную звездную величину:
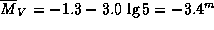 .
На первый взгляд, приведенных в условии задачи данных недостаточно
для ее решения -- нужно знать среднюю видимую звездную величину
.
На первый взгляд, приведенных в условии задачи данных недостаточно
для ее решения -- нужно знать среднюю видимую звездную величину
 Cep, которая нам неизвестна. Однако неявно эта
информация есть:
Cep, которая нам неизвестна. Однако неявно эта
информация есть: 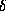 Cep, как показывает ее название, является
четвертой по яркости звездой в созвездии Цефея. Но Цефей --
созвездие не из ярких, его звезды значительно, на полторы -- две
звездных величины слабее звезд ковша Большой Медведицы.
Поэтому в качестве разумной оценки среднего значения блеска
Cep, как показывает ее название, является
четвертой по яркости звездой в созвездии Цефея. Но Цефей --
созвездие не из ярких, его звезды значительно, на полторы -- две
звездных величины слабее звезд ковша Большой Медведицы.
Поэтому в качестве разумной оценки среднего значения блеска
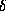 Cep можно принять 4
Cep можно принять 4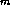 . Теперь по известной формуле
. Теперь по известной формуле
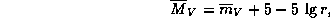
где r -- в парсеках, находим 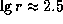 ,
откуда
,
откуда 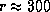 пк.
пк.
Несмотря на столь значительное расстояние,  Cep
прекрасно видна простым глазом. Это сверхгигант. Cветимость
Cep
прекрасно видна простым глазом. Это сверхгигант. Cветимость
 Cep, как и всех цефеид, очень высока.
Ведь иначе цефеиды не могли бы служить "маяками Вселенной"!
Cep, как и всех цефеид, очень высока.
Ведь иначе цефеиды не могли бы служить "маяками Вселенной"!
 13.3
Естественно предположить, что частота колебаний блеска цефеиды
13.3
Естественно предположить, что частота колебаний блеска цефеиды
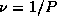 меняется с годовым периодом
за счет эффекта Доплера, обусловленного орбитальным движением Земли.
Мы имеем:
меняется с годовым периодом
за счет эффекта Доплера, обусловленного орбитальным движением Земли.
Мы имеем:

где 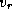 -- максимальная величина проекции вектора орбитальной
скорости Земли
-- максимальная величина проекции вектора орбитальной
скорости Земли  на прямую Солнце -- цефеида.
Отсюда
на прямую Солнце -- цефеида.
Отсюда
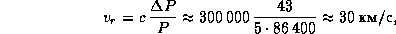
что совпадает с орбитальной скоростью Земли.
Заключаем, что звезда лежит в плоскости эклиптики.
Период максимален, когда направление на звезду противоположно направлению
движения Земли.
Но, как легко сообразить (сделайте соответствующий чертеж), в конце
декабря (зимнее солнцестояние) вектор скорости Земли направлен
в точку осеннего равноденствия.
Поэтому звезда находится на небе неподалеку от точки весеннего
равноденствия, и ее экваториальные координаты
 ,
, 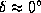 .
.
 13.4
По определению болометрической звездной величины имеем
13.4
По определению болометрической звездной величины имеем
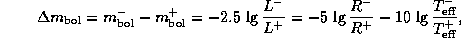
где 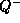 и
и 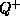 -- значения величины Q
в минимуме и в максимуме блеска, соответственно.
Изменения радиуса и
блеска происходят, грубо говоря, в противофазе, так что в максимуме
блеска радиус минимален. Положим поэтому
-- значения величины Q
в минимуме и в максимуме блеска, соответственно.
Изменения радиуса и
блеска происходят, грубо говоря, в противофазе, так что в максимуме
блеска радиус минимален. Положим поэтому
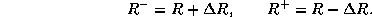
Подставляя значения
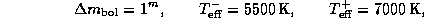
для относительного изменения радиуса цефеиды в ходе
пульсаций находим
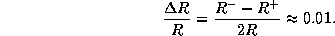
В действительности изменения блеска и радиуса у цефеид происходят не
точно в противофазе -- имеется фазовое запаздывание, которым мы
пренебрегли.
Однако полученная
оценка 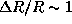 % близка к реальному изменению
радиуса. Как видим, цефеиды совершают малые колебания.
% близка к реальному изменению
радиуса. Как видим, цефеиды совершают малые колебания.
Главная мораль этой задачи: расхожее представление, будто основной причиной колебаний блеска цефеид является изменение их размеров в ходе пульсаций, ошибочно. Главный вклад в колебания блеска дают вариации температуры, а не радиуса!
 13.5
Из третьего закона Кеплера находим большую полуось орбиты двойной системы
13.5
Из третьего закона Кеплера находим большую полуось орбиты двойной системы
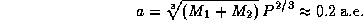
Здесь P выражено в годах, а массы -- в массах Солнца.
Далее, расстояние от пульсара до центра масс системы равно
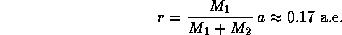
Зная r и P, можем оценить скорость орбитального движения пульсара:
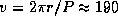 км/с.
Из-за эффекта Доплера период пульсаций (обратный частоте) изменяется,
причем амплитуда относительного изменения периода равна
км/с.
Из-за эффекта Доплера период пульсаций (обратный частоте) изменяется,
причем амплитуда относительного изменения периода равна
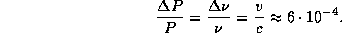
На самом деле эффект наблюдается как запаздывание (или опережение)
времени прихода импульсов. Оно весьма значительно. Путь в
2r=0.34 а.е. излучение пульсара проходит за
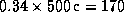 с.
Это и есть максимальное запаздывание (опережение).
Полное число импульсов, которое
испускает наш пульсар за такое время, составляет 1700. Это есть
недостача (или избыток) числа импульсов при перемещении пульсара от
самой дальней от наблюдателя точки орбиты до самой ближней (или
наоборот). За полупериод, т.е. за
с.
Это и есть максимальное запаздывание (опережение).
Полное число импульсов, которое
испускает наш пульсар за такое время, составляет 1700. Это есть
недостача (или избыток) числа импульсов при перемещении пульсара от
самой дальней от наблюдателя точки орбиты до самой ближней (или
наоборот). За полупериод, т.е. за
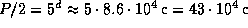 пульсар испускает
пульсар испускает 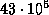 импульсов.
Среднее за полупериод запаздывание (или опережение) составляет, таким образом,
импульсов.
Среднее за полупериод запаздывание (или опережение) составляет, таким образом,
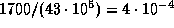 .
Ясно, что так как период пульсаций
меняется синусоидально, то для получения максимальной величины надо
это число поделить на среднее от одной полуволны синусоиды
.
Ясно, что так как период пульсаций
меняется синусоидально, то для получения максимальной величины надо
это число поделить на среднее от одной полуволны синусоиды

В результате получаем то же число (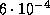 ), которое было
найдено выше другим путем.
), которое было
найдено выше другим путем.
По сути дела, описанное запаздывание времен прихода импульсов у рентгеновских пульсаров -- это тот же эффект, по которому Ремер в 17 веке впервые измерил скорость света. В его распоряжении была эфемерида, рассчитанная по наблюдениям затмений Ио в период, когда Юпитер был в противостоянии, и наблюдения затмений Ио Юпитером, находящимся в соединении с Солнцем. Эти наблюдения показывали, что затмения спутника запаздывают по сравнению с эфемеридой. Ремер правильно объяснил запаздывание конечностью скорости распространения света и получил правильную по порядку величины оценку этой скорости.
 13.6
В задаче
13.6
В задаче  мы оценили угол, под которым с
мы оценили угол, под которым с 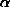 Cen видна
большая полуось орбиты Юпитера, и нашли, что он равен примерно
Cen видна
большая полуось орбиты Юпитера, и нашли, что он равен примерно 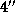 .
Оценим теперь видимую звездную величину Юпитера для наблюдателя на
.
Оценим теперь видимую звездную величину Юпитера для наблюдателя на
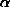 Cen. Радиус Юпитера составляет примерно
Cen. Радиус Юпитера составляет примерно 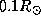 (его нет во "Вселенной в числах", но его легко можно вычислить по
имеющимся там данным о массе и средней плотности Юпитера).
Видимую звездную величину Юпитера для наблюдателя на Земле можно найти
точно так же, как мы нашли звездную величину Европы в задаче
(его нет во "Вселенной в числах", но его легко можно вычислить по
имеющимся там данным о массе и средней плотности Юпитера).
Видимую звездную величину Юпитера для наблюдателя на Земле можно найти
точно так же, как мы нашли звездную величину Европы в задаче  .
Если считать альбедо Юпитера равным 1, то найдем, что в противостоянии
.
Если считать альбедо Юпитера равным 1, то найдем, что в противостоянии
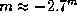 , что мало отличается от истинного значения
, что мало отличается от истинного значения 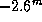 .
Расстояние до
.
Расстояние до 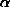 Cen -- 1.3 пк, или
Cen -- 1.3 пк, или 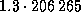 а.е.
При наблюдении с такого расстояния видимая звездная величина Юпитера,
если бы он находился в соединении с Солнцем, была бы равна
а.е.
При наблюдении с такого расстояния видимая звездная величина Юпитера,
если бы он находился в соединении с Солнцем, была бы равна
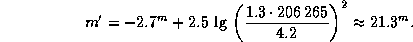
Число 4.2, появившееся здесь, -- это расстояние до Юпитера в противостоянии
(в а.е.).
В элонгации (для наблюдателя с  Cen) звездная величина
Юпитера будет еще примерно на звездную
величину больше из-за
влияния его фазы.
(Для наших целей аккуратно учитывать это обстоятельство нет нужды).
Солнце же с
Cen) звездная величина
Юпитера будет еще примерно на звездную
величину больше из-за
влияния его фазы.
(Для наших целей аккуратно учитывать это обстоятельство нет нужды).
Солнце же с  Cen имеет звездную величину
Cen имеет звездную величину
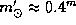 (проверьте).
(проверьте).
Таким образом, с одной стороны, угловое расстояние между Солнцем и Юпитером
при наблюдении с 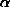 Cen достаточно, чтобы его можно
было разрешить с помощью телескопа,
но, с другой стороны, разность их звездных величин настолько велика,
что слабый Юпитер скорее всего не будет виден вблизи гораздо
более яркого Солнца (см. задачу
Cen достаточно, чтобы его можно
было разрешить с помощью телескопа,
но, с другой стороны, разность их звездных величин настолько велика,
что слабый Юпитер скорее всего не будет виден вблизи гораздо
более яркого Солнца (см. задачу  про галилеевы спутники
Юпитера, точнее, про Европу).
про галилеевы спутники
Юпитера, точнее, про Европу).
У наших коллег-астрономов с 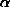 Cen есть, впрочем, и другие
пути обнаружить существование Юпитера -- длительные прецизионные
измерения малых вариаций лучевой скорости и собственного движения
Солнца (см. следующую задачу).
Cen есть, впрочем, и другие
пути обнаружить существование Юпитера -- длительные прецизионные
измерения малых вариаций лучевой скорости и собственного движения
Солнца (см. следующую задачу).
 13.7
Для простоты решим задачу в предположении, что вокруг Солнца обращается
только одна планета -- Юпитер с массой
13.7
Для простоты решим задачу в предположении, что вокруг Солнца обращается
только одна планета -- Юпитер с массой 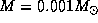 и
орбитальной скоростью 13 км/с (см. задачу
и
орбитальной скоростью 13 км/с (см. задачу  ).
Отношение скоростей движения двух тел вокруг общего центра масс
равно отношению их масс, в нашем случае -- 1:1000.
Поэтому скорость движения центра Солнца составляет
).
Отношение скоростей движения двух тел вокруг общего центра масс
равно отношению их масс, в нашем случае -- 1:1000.
Поэтому скорость движения центра Солнца составляет 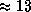 м/с.
Именно такой (или лучше хотя бы раза в два более высокой)
должна быть точность определения лучевых скоростей,
чтобы астроном-инопланетянин, живущий в плоскости эклиптики,
по измерениям лучевых скоростей Солнца
мог заподозрить существование Солнечной системы.
Для астронома же,
изучающего движение Солнца с
м/с.
Именно такой (или лучше хотя бы раза в два более высокой)
должна быть точность определения лучевых скоростей,
чтобы астроном-инопланетянин, живущий в плоскости эклиптики,
по измерениям лучевых скоростей Солнца
мог заподозрить существование Солнечной системы.
Для астронома же,
изучающего движение Солнца с 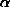 Cen, амплитуда изменений его
лучевой скорости будет меньше 13 м/с, а именно,
Cen, амплитуда изменений его
лучевой скорости будет меньше 13 м/с, а именно, 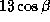 м/с
м/с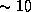 м/с. Здесь
м/с. Здесь 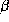 -- эклиптическая широта
-- эклиптическая широта
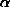 Cen (оцените ее самостоятельно по координатам
Cen (оцените ее самостоятельно по координатам 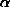 Cen
или даже просто по звездной карте).
Cen
или даже просто по звездной карте).
Интересно, что в 1995-1996 гг. у нескольких звезд, подобных Солнцу
(70Vir, 47UMa и др.),
были обнаружены планеты с массами, близкими к массе Юпитера.
Чтобы сделать это выдающееся открытие,
потребовалось разработать методику и создать специальную
аппаратуру, позволившие измерять лучевые скорости с точностью порядка 10 м/с.
Измерения велись в течение нескольких лет.
С 1994 г. лучевые скорости стали измерять уже с точностью
до 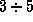 м/с.
Хороший спринтер пробегает стометровку со скоростью около
10 м/с, а 3 м/с -- это бег трусцой.
м/с.
Хороший спринтер пробегает стометровку со скоростью около
10 м/с, а 3 м/с -- это бег трусцой.
К моменту сдачи этого задачника в печать (август 1997 г.) наличие планет с массами от 0.5 до 13 масс Юпитера надежно установлено у 9 звезд.
Когда вы будете это читать, эти данные, несомненно, уже устареют. С состоянием дел на сегодняшний день (когда бы это ни происходило!) вы можете ознакомиться по постоянно обновляемой электронной "Энциклопедии внесолнечных планет", доступной в Интернете по адресу
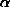 Cen оценим
с помощью известного соотношения
Cen оценим
с помощью известного соотношения

 -- параллакс
-- параллакс 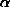 Cen. Так как
Cen. Так как 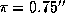 , то,
подставляя
, то,
подставляя
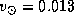 км/с, находим
км/с, находим 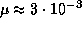 угл. сек./год.
угл. сек./год.
Обнаружение планет около нескольких звезд по измерениям лучевых скоростей, о чем говорилось выше, было подтверждено выявлением по данным, полученным ранее на астрометрическом спутнике HIPPARCOS, периодических изменений их собственных движений.


