


Next: Звездные величины
Up: Задачи
Previous: Всемирное тяготение
Решения
 6.1
В подсолнечной точке темп притока энергии равен
6.1
В подсолнечной точке темп притока энергии равен 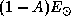 , где
, где
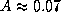 -- альбедо Луны,
-- альбедо Луны,
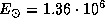 эрг/(см2c) -- солнечная постоянная.
Отток энергии происходит за счет излучения нагретого поверхностного
слоя почвы (в ИК-диапазоне), темп которого равен
эрг/(см2c) -- солнечная постоянная.
Отток энергии происходит за счет излучения нагретого поверхностного
слоя почвы (в ИК-диапазоне), темп которого равен
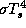 , где
, где 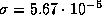 -- постоянная Стефана
(индекс s у
-- постоянная Стефана
(индекс s у 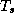 -- от surface, т.е. поверхность). Приравнивая
темпы нагрева и охлаждения, получаем
-- от surface, т.е. поверхность). Приравнивая
темпы нагрева и охлаждения, получаем

откуда 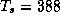 K, или 115o по Цельсию, так что босиком не
походишь -- обожжешь ступни. Эта оценка слегка завышена. Она была бы
строго верна, если бы Луна всегда была обращена одной стороной к
Солнцу (а не к Земле). Однако так как вращение Луны вокруг оси происходит
медленно, ошибка должна быть невелика.
K, или 115o по Цельсию, так что босиком не
походишь -- обожжешь ступни. Эта оценка слегка завышена. Она была бы
строго верна, если бы Луна всегда была обращена одной стороной к
Солнцу (а не к Земле). Однако так как вращение Луны вокруг оси происходит
медленно, ошибка должна быть невелика.
 6.2
Будут очень-очень сильно мерзнуть ноги. Из-за различия в альбедо
отношение абсолютных
температур на месте, залитом краской, и на соседнем лунном грунте
будет близко к
6.2
Будут очень-очень сильно мерзнуть ноги. Из-за различия в альбедо
отношение абсолютных
температур на месте, залитом краской, и на соседнем лунном грунте
будет близко к 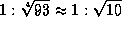 (см. формулу в решении задачи
(см. формулу в решении задачи  ). Если
у обычного лунного грунта (альбедо A=0.07) в подсолнечной точке
температура равна 388 K (см. предыдущую задачу), то в луже краски
она будет
). Если
у обычного лунного грунта (альбедо A=0.07) в подсолнечной точке
температура равна 388 K (см. предыдущую задачу), то в луже краски
она будет 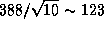 K, или
K, или 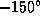 по
Цельсию -- жуткий мороз! (А железный лист в условии задачи зачем
понадобился, как вы думаете?)
по
Цельсию -- жуткий мороз! (А железный лист в условии задачи зачем
понадобился, как вы думаете?)
 6.3
На единицу поверхности планеты в "подсолнечной" точке
падает поток
6.3
На единицу поверхности планеты в "подсолнечной" точке
падает поток 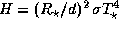 ,
где
,
где 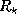 -- радиус звезды,
а d -- расстояние от нее до планеты.
Из этого потока доля 1-A,
поглощаемая поверхностью планеты, идет на ее нагрев.
Приравнивая скорости притока и оттока тепла в "подсолнечной" точке,
получаем
-- радиус звезды,
а d -- расстояние от нее до планеты.
Из этого потока доля 1-A,
поглощаемая поверхностью планеты, идет на ее нагрев.
Приравнивая скорости притока и оттока тепла в "подсолнечной" точке,
получаем
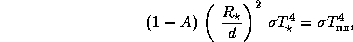
откуда для температуры 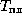 в "подсолнечной" точке находим
в "подсолнечной" точке находим
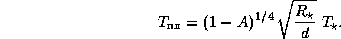
Значение d найдем, приравнивая центробежную силу к силе притяжения
планеты к звезде, что дает

где P -- период обращения планеты. Эрудиты, помнящие наизусть
третий закон Кеплера, точнее, коэффициент пропорциональности в
соотношении 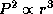 , могли бы написать это сразу.
, могли бы написать это сразу.
Подставляя это выражение для d через P в формулу для
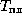 , получаем
, получаем

Единственный параметр звезды, помимо ее температуры,
который входит в эту формулу, это ее средняя плотность
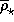 .
.
По условию задачи, температура на планете должна
быть такой же, как на Луне. Последняя, очевидно, также дается
полученным только что выражением, в котором следует положить
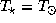 и
и 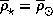 ,
а P взять равным 1 году.
Приравнивая температуры на планете и на Луне, для периода обращения
планеты в годах получаем следующее простое выражение:
,
а P взять равным 1 году.
Приравнивая температуры на планете и на Луне, для периода обращения
планеты в годах получаем следующее простое выражение:
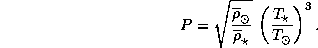
Подставив числа, найдем, что, например, для звезды класса A0
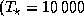 K,
K,
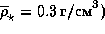 период
составляет около 10 лет.
период
составляет около 10 лет.
Далее, так как величина падающего
потока пропорциональна косинусу зенитного расстояния звезды z, то
зависимость температуры на поверхности лишенной атмосферы планеты от
z имеет вид
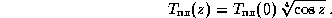
Выражение для P, полученное выше, позволяет немного
пофантазировать о жизни на других мирах.
Очевидно, что оно дает продолжительность года на планете с тем же
температурным режимом, что
и у Земли, которая обращается вокруг звезды с известной температурой и
средней плотностью. Данные о 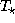 и
и 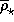 для звезд разных спектральных классов можно найти у Аллена [1].
Оказывается, например,
что если бы Земля обращалась не вокруг Солнца, а вокруг звезды класса
M5V (
для звезд разных спектральных классов можно найти у Аллена [1].
Оказывается, например,
что если бы Земля обращалась не вокруг Солнца, а вокруг звезды класса
M5V (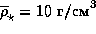 ,
,
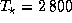 K), то
чтобы на ней можно было сносно жить -- не
замерзнуть и не изжариться -- продолжительность года
должна была бы составлять всего
K), то
чтобы на ней можно было сносно жить -- не
замерзнуть и не изжариться -- продолжительность года
должна была бы составлять всего 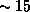 земных суток.
Впадать в долгую зимнюю спячку медведям не удалось бы!
земных суток.
Впадать в долгую зимнюю спячку медведям не удалось бы!
 6.4
Для ионизации атома водорода требуется энергия
6.4
Для ионизации атома водорода требуется энергия 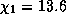 эВ.
Поэтому число атомов водорода
эВ.
Поэтому число атомов водорода 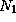 , которое может быть ионизовано
за счет кинетической энергии движения Земли, равно
, которое может быть ионизовано
за счет кинетической энергии движения Земли, равно

где v=30 км/с -- скорость движения Земли, M -- ее масса. Далее,
число атомов водорода в газовом облаке с массой M
равно 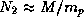 ,
где
,
где 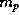 -- масса протона. Подставляя известные числовые
значения физических величин, находим отношение
-- масса протона. Подставляя известные числовые
значения физических величин, находим отношение

которое оказывается хотя и порядка, но все же меньше единицы.
Таким образом, кинетической энергии движения Земли по орбите не
достаточно, чтобы ионизовать облако водорода с массой, равной массе
Земли.
Дадим другой вариант решения. Как показывается в задаче  , нуклон, движущийся со скоростью 1500 км/с, имеет энергию
около 10кэВ. При скорости движения в 30 км/с кинетическая энергия
нуклона будет в
, нуклон, движущийся со скоростью 1500 км/с, имеет энергию
около 10кэВ. При скорости движения в 30 км/с кинетическая энергия
нуклона будет в 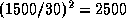 раз меньше, или около
4эВ, что составляет 0.3 от энергии связи атома водорода (13.6эВ).
Отсюда непосредственно следует, в согласии с полученным выше, что
кинетической энергии движения Земли хватит на ионизацию массы
водорода, составляющей 0.3 ее собственной массы.
раз меньше, или около
4эВ, что составляет 0.3 от энергии связи атома водорода (13.6эВ).
Отсюда непосредственно следует, в согласии с полученным выше, что
кинетической энергии движения Земли хватит на ионизацию массы
водорода, составляющей 0.3 ее собственной массы.
Кинетическая энергия протона равна 1 эВ, если он движется со
скоростью 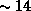 км/с.
км/с.
 6.5
Один способ решения см. во вводных замечаниях к задачнику.
А вот другое решение.
Всякий знает, что атмосферное давление составляет
6.5
Один способ решения см. во вводных замечаниях к задачнику.
А вот другое решение.
Всякий знает, что атмосферное давление составляет 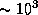 г/см2.
Поэтому масса столба воздуха сечением 1 см2
равна
г/см2.
Поэтому масса столба воздуха сечением 1 см2
равна 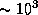 г. Умножив это на площадь поверхности Земли,
получим искомую массу атмосферы.
Осталось поделить результат на массу Земли.
г. Умножив это на площадь поверхности Земли,
получим искомую массу атмосферы.
Осталось поделить результат на массу Земли.
К сожалению, при таком решении приходится делать несколько
не очень приятных умножений, а в конце еще и деление.
Можно дать и такое решение, в котором вычисления сведены к минимуму.
Вес вертикального столба воздуха равен весу столба воды высотой 10 м --
надеемся, вы это знаете.
Плотность воды 1 г/см3, а средняя плотность Земли -- 5.5 г/см3.
Поэтому воздух давит так же, как и слой вещества
плотностью 5.5 г/см3, имеющий толщину 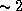 м.
Далее, из формулы
м.
Далее, из формулы

следует, что

Отсюда в уме находим, что при
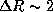 м будет
м будет 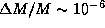 .
.
 6.6
Точность "параллельного приближения" -- угловой диаметр Солнца,
6.6
Точность "параллельного приближения" -- угловой диаметр Солнца, 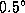 .
А описанная картина объясняется так же, как и кажущаяся сходимость
параллельных рельсов или расходимость траекторий метеоров
из радианта -- явлением перспективы.
.
А описанная картина объясняется так же, как и кажущаяся сходимость
параллельных рельсов или расходимость траекторий метеоров
из радианта -- явлением перспективы.
 6.7
Высота однородной атмосферы Земли равна примерно 8 км. Это означает, что
плотность воздуха
6.7
Высота однородной атмосферы Земли равна примерно 8 км. Это означает, что
плотность воздуха 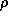 убывает с высотой по закону (так называемая
барометрическая формула; кстати, как вы думаете, почему она так называется?)
убывает с высотой по закону (так называемая
барометрическая формула; кстати, как вы думаете, почему она так называется?)

где h -- высота в км.
Плотность воздуха падает в пять раз на высоте около 13 км (проверьте!).
Поэтому, если масса атмосферы уменьшится впятеро, цвет неба
станет темно-синим, примерно таким, как из окна
пассажирского воздушного лайнера после набора высоты.
Если же масса атмосферы возрастет в 5 раз, то небо днем станет
желтовато-оранжевым. Дело в том, что по закону Рэлея оптическая
толщина атмосферы обратно пропорциональна 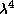 . Для синих
лучей она окажется больше единицы, и это излучение будет сильно ослаблено.
Восход и закат Солнца едва ли будут видны -- при приближении к
горизонту диск Солнца будет постепенно становиться все менее ярким, и
еще до достижения горизонта он скорее всего перестанет быть виден.
Ночью звезд на небе будет совсем мало, и они будут красновато-желтыми.
Вблизи горизонта, на зенитных расстояниях
. Для синих
лучей она окажется больше единицы, и это излучение будет сильно ослаблено.
Восход и закат Солнца едва ли будут видны -- при приближении к
горизонту диск Солнца будет постепенно становиться все менее ярким, и
еще до достижения горизонта он скорее всего перестанет быть виден.
Ночью звезд на небе будет совсем мало, и они будут красновато-желтыми.
Вблизи горизонта, на зенитных расстояниях 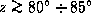 ,
их вовсе не будет видно, так как оптическая толщина по лучу зрения
,
их вовсе не будет видно, так как оптическая толщина по лучу зрения
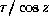 будет
будет 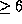 .
.
 6.8
Очевидно, что максимум яркости неба достигается при оптической толщине
атмосферы
6.8
Очевидно, что максимум яркости неба достигается при оптической толщине
атмосферы  порядка единицы. Действительно, если
порядка единицы. Действительно, если 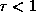 , то
чем меньше
, то
чем меньше  , тем большая
доля фотонов проходит сквозь атмосферу не рассеиваясь и,
следовательно, не дает вклада в яркость неба.
Поэтому при малых
, тем большая
доля фотонов проходит сквозь атмосферу не рассеиваясь и,
следовательно, не дает вклада в яркость неба.
Поэтому при малых  яркость неба растет с
яркость неба растет с  . А при
. А при 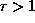 с ростом
с ростом  быстро увеличивается
доля фотонов, которые, испытав многократные рассеяния в атмосфере,
отражаются ею обратно в космическое
пространство и не доходят до поверхности Земли. Здесь с ростом
быстро увеличивается
доля фотонов, которые, испытав многократные рассеяния в атмосфере,
отражаются ею обратно в космическое
пространство и не доходят до поверхности Земли. Здесь с ростом  яркость неба должна убывать. Однако точный расчет того
яркость неба должна убывать. Однако точный расчет того
 , при котором для заданного зенитного расстояния Солнца
падающий на поверхность Земли поток рассеянного атмосферой излучения
максимален -- это очень непростая задача. Во всяком случае, авторам
не только неизвестен ответ, но неизвестно даже, где его можно найти
в литературе!
, при котором для заданного зенитного расстояния Солнца
падающий на поверхность Земли поток рассеянного атмосферой излучения
максимален -- это очень непростая задача. Во всяком случае, авторам
не только неизвестен ответ, но неизвестно даже, где его можно найти
в литературе!
 6.9
Химический состав солнечной атмосферы определяется по интенсивностям
фраунгоферовых линий. При прохождении сквозь слой облаков солнечное
излучение испытывает многократные рассеяния, в ходе которых
информация о первоначальном направлении его распространения полностью
замывается. Поэтому, когда небо затянуто тяжелыми тучами, сказать,
где находится Солнце, нельзя. Однако спектральный состав излучения,
прошедшего сквозь облака, почти не меняется. В частности,
интенсивности фраунгоферовых линий (по отношению к соседнему
континууму) те же, что и в ясный день. Правда, из-за рассеяний на
частицах облаков -- водяных каплях или снежинках -- траектория луча
становится ломаной линией, и в результате оптический путь вдоль
луча увеличивается. Интенсивность теллурических линий будет поэтому
увеличена. Однако если наш дисциплинированный астроном будет
наблюдать достаточно долго, он сумеет отделить теллурические линии от
фраунгоферовых. Из-за изменения высоты Солнца теллурические линии
будут со временем менять свою интенсивность, фраунгоферовы же --
нет. Итак, даже когда Солнца из-за облаков не видно, химический
состав его атмосферы можно определить!
6.9
Химический состав солнечной атмосферы определяется по интенсивностям
фраунгоферовых линий. При прохождении сквозь слой облаков солнечное
излучение испытывает многократные рассеяния, в ходе которых
информация о первоначальном направлении его распространения полностью
замывается. Поэтому, когда небо затянуто тяжелыми тучами, сказать,
где находится Солнце, нельзя. Однако спектральный состав излучения,
прошедшего сквозь облака, почти не меняется. В частности,
интенсивности фраунгоферовых линий (по отношению к соседнему
континууму) те же, что и в ясный день. Правда, из-за рассеяний на
частицах облаков -- водяных каплях или снежинках -- траектория луча
становится ломаной линией, и в результате оптический путь вдоль
луча увеличивается. Интенсивность теллурических линий будет поэтому
увеличена. Однако если наш дисциплинированный астроном будет
наблюдать достаточно долго, он сумеет отделить теллурические линии от
фраунгоферовых. Из-за изменения высоты Солнца теллурические линии
будут со временем менять свою интенсивность, фраунгоферовы же --
нет. Итак, даже когда Солнца из-за облаков не видно, химический
состав его атмосферы можно определить!
Главное, что мы хотели подчеркнуть: при многократных рассеяниях
замывается не вся информация. Это важно, так как указывает на
принципиальную возможность извлечения из приходящего от звезд и
планет излучения сведений о тех слоях их атмосфер, которые
непосредственно не видны. "Кухня" этого далеко не проста, и говорить
о ней здесь было бы неуместно.
 6.10
Кажется почти очевидным, что при наблюдении с горы Солнце будет
ярче -- но это неверно. Из рисунка понятно, что для наблюдателя A,
находящегося на уровне моря, ослабление солнечного излучения
атмосферой будет меньше, чем для наблюдателя B, стоящего на
горе. Приводимый ниже расчет показывает, что разница в яркости будет
весьма ощутимой: на
6.10
Кажется почти очевидным, что при наблюдении с горы Солнце будет
ярче -- но это неверно. Из рисунка понятно, что для наблюдателя A,
находящегося на уровне моря, ослабление солнечного излучения
атмосферой будет меньше, чем для наблюдателя B, стоящего на
горе. Приводимый ниже расчет показывает, что разница в яркости будет
весьма ощутимой: на 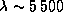
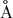 (максимум чувствительности
глаза) различие будет по меньшей мере 20-кратным.
(максимум чувствительности
глаза) различие будет по меньшей мере 20-кратным.
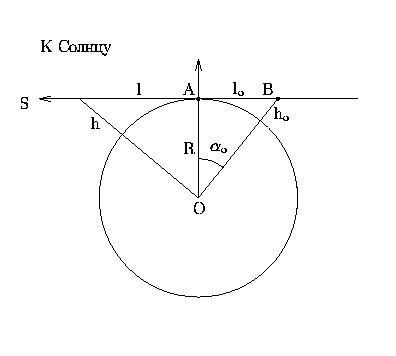 Сначала дадим грубую оценку, которую потом уточним.
Будем считать атмосферу однородным сферическим слоем толщиной h = 8 км.
Тогда для наблюдателя, находящегося в точке A (на уровне моря),
длину пути l горизонтального луча в атмосфере можно определить по теореме
Пифагора (см. рис.):
Сначала дадим грубую оценку, которую потом уточним.
Будем считать атмосферу однородным сферическим слоем толщиной h = 8 км.
Тогда для наблюдателя, находящегося в точке A (на уровне моря),
длину пути l горизонтального луча в атмосфере можно определить по теореме
Пифагора (см. рис.):
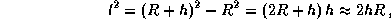
где R -- радиус Земли.
Отсюда
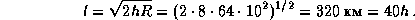
На первый взгляд это число представляется неожиданно большим --
но вспомните, что Земля кажется нам плоской даже с высокой горы.
Из полученной оценки следует, что на восходе и на закате Солнце
вполне могут скрывать тучи, находящиеся от нас в паре сотен километров.
Мало кто это знает.
Аналогичным образом нетрудно найти, что дополнительный путь 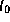 ,
который солнечные лучи проходят в атмосфере при наблюдении восхода
с горы высотой
,
который солнечные лучи проходят в атмосфере при наблюдении восхода
с горы высотой 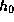 , составляет
, составляет

При 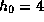 км мы имеем
км мы имеем 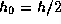 , так что
, так что

Оптическая толщина безоблачной атмосферы по нормали
на длине волны 5500 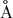 составляет
составляет 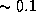 (в действительности даже несколько больше, см. ниже).
По касательной, как мы только что убедились, она должна
быть в 40 раз больше, т.е.
(в действительности даже несколько больше, см. ниже).
По касательной, как мы только что убедились, она должна
быть в 40 раз больше, т.е. 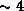 .
Поэтому в момент восхода солнечное излучение на
.
Поэтому в момент восхода солнечное излучение на
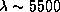
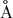 ослабляется атмосферой в
ослабляется атмосферой в
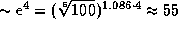 раз
(или на
раз
(или на 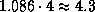 звездных величины).
На пути от A до B луч ослабляется дополнительно в
звездных величины).
На пути от A до B луч ослабляется дополнительно в
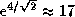 раз, так что диск Солнца
при наблюдении восхода с высокой горы оказывается гораздо менее
ярким, чем с корабля.
раз, так что диск Солнца
при наблюдении восхода с высокой горы оказывается гораздо менее
ярким, чем с корабля.
Полученное только что число 17 -- не более чем оценка, к тому же
довольно грубая.
Действительно, значение оптической толщины атмосферы по нормали,
которое мы использовали (0.1), относится к чисто молекулярной атмосфере.
Однако в атмосфере происходит также рассеяние солнечного излучения на
частицах аэрозоля, так что действительная оптическая толщина
несколько больше, причем она колеблется ото дня ко дню.
Очень существенно, что для нахождения стоящей в показателе
экспоненты оптической толщины атмосферы вдоль горизонтально идущего луча
мы должны вертикальную оптическую толщину умножить на большое число (40).
Поэтому даже незначительное отличие в принятом значении
оптической толщины атмосферы по нормали ведет к большому отличию
в яркости Солнца в момент восхода.
Так, если бы оптическую толщину по нормали мы приняли бы равной не
0.10, а 0.13, то нашли бы, что солнечные лучи на
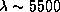
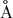 ослабляются при наблюдении восхода и заката с уровня
моря в
ослабляются при наблюдении восхода и заката с уровня
моря в 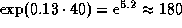 раз.
При наблюдении с горы высотой
раз.
При наблюдении с горы высотой 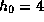 км яркость диска Солнца в момент
восхода уменьшалась бы дополнительно в
км яркость диска Солнца в момент
восхода уменьшалась бы дополнительно в
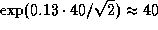 раз.
Как видим, полученные выше оценки, относящиеся к чисто газовой атмосфере,
вполне могут давать яркость Солнца в момент восхода с ошибкой
в несколько раз.
раз.
Как видим, полученные выше оценки, относящиеся к чисто газовой атмосфере,
вполне могут давать яркость Солнца в момент восхода с ошибкой
в несколько раз.
По сравнению с этим поправка, вызванная учетом неоднородности
атмосферы, малосущественна (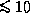 % в горизонтальной оптической толщине).
Можно считать, что плотность в атмосфере меняется с высотой h по
барометрическому закону
% в горизонтальной оптической толщине).
Можно считать, что плотность в атмосфере меняется с высотой h по
барометрическому закону

где H -- параметр (так называемая шкала высот),
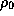 -- плотность воздуха на уровне моря.
Рассмотрим сначала случай наблюдения из точки A, т.е. с уровня моря.
Тогда воздушная масса на горизонтальном луче оказывается равной
-- плотность воздуха на уровне моря.
Рассмотрим сначала случай наблюдения из точки A, т.е. с уровня моря.
Тогда воздушная масса на горизонтальном луче оказывается равной
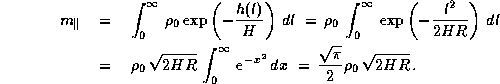
Масса же на вертикальном луче равна, очевидно,
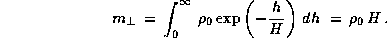
Отношение этих двух воздушных масс дает отношение оптических толщин атмосферы
по горизонтали и по вертикали:

что отличается от результата, полученного в предположении однородности
атмосферы, на множитель 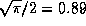 .
Его отличие от единицы нужно было бы учитывать, если бы
оптическая толщина атмосферы по нормали была бы известна с точностью
.
Его отличие от единицы нужно было бы учитывать, если бы
оптическая толщина атмосферы по нормали была бы известна с точностью
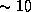 %, чего из-за переменной запыленности воздуха на самом деле нет.
%, чего из-за переменной запыленности воздуха на самом деле нет.
Убедитесь самостоятельно, что дополнительный оптический
путь луча от A к B
составляет долю

где

от оптического пути вдоль луча AS.
Появившийся здесь интеграл
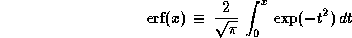
называется функцией ошибок, или интегралом вероятностей.
Он не выражается через элементарные функции.
Его таблицы есть в любом курсе теории вероятностей, однако не
спешите их доставать.
В нашем случае оценить значение этого интеграла не составляет труда.
Мы имеем 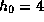 км = H/2, так что
км = H/2, так что 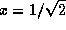 .
Разлагая экспоненту в ряд и интегрируя затем этот ряд почленно,
находим, что
.
Разлагая экспоненту в ряд и интегрируя затем этот ряд почленно,
находим, что
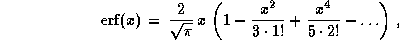
откуда получаем, что 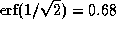 .
Это очень близко к числу
.
Это очень близко к числу 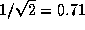 , полученному нами ранее для
отношения воздушных масс на пути AB и на луче AS в предположении,
что атмосфера однородна.
, полученному нами ранее для
отношения воздушных масс на пути AB и на луче AS в предположении,
что атмосфера однородна.
Еще один эффект, влияние которого в принципе нужно было бы учитывать, --
это рефракция.
Ограничиваясь качественной стороной дела, можно утверждать,
что влияние рефракции будет делать Солнце для "горного" наблюдателя
еще менее ярким, чем для "морского" (поймите, почему).
Вот иная формулировка наших основных результатов.
По условию задачи Солнце наблюдается
на видимом горизонте, а не на математическом.
Для "горного" наблюдателя понижение горизонта составляет
всего около 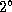 (покажите это, вычислив угол
(покажите это, вычислив угол 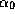 ),
однако это приводит к тому, что солнечные лучи проходят
дополнительный путь
),
однако это приводит к тому, что солнечные лучи проходят
дополнительный путь 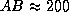 км, что увеличивает
массу и оптическую толщину столба воздуха на их пути
почти на 70% и делает Солнце значительно менее ярким
(экспонента -- это не линейная функция!).
Но когда восходящее Солнце достигнет математического горизонта,
оно будет уже в
км, что увеличивает
массу и оптическую толщину столба воздуха на их пути
почти на 70% и делает Солнце значительно менее ярким
(экспонента -- это не линейная функция!).
Но когда восходящее Солнце достигнет математического горизонта,
оно будет уже в 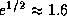 раза более
ярким, чем в случае его наблюдения на горизонте с уровня моря.
Убедитесь в этом самостоятельно.
раза более
ярким, чем в случае его наблюдения на горизонте с уровня моря.
Убедитесь в этом самостоятельно.
Побочным результатом проведенного в этой задаче обсуждения
служит следующее неожиданное на первый взгляд утверждение:
ни один космонавт не мог видеть простым глазом ни одной звезды
в момент ее выхода из-за края Земли!
 6.11
Интенсивность прямого излучения Солнца у горизонта при сделанных
допущениях есть
6.11
Интенсивность прямого излучения Солнца у горизонта при сделанных
допущениях есть 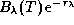 , где
, где
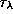 -- оптическая толщина атмосферы вдоль горизонтального
луча. При молекулярном рассеянии
-- оптическая толщина атмосферы вдоль горизонтального
луча. При молекулярном рассеянии 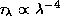 (закон Рэлея). Положим
(закон Рэлея). Положим

где 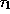 -- горизонтальная оптическая толщина атмосферы на длине
волны
-- горизонтальная оптическая толщина атмосферы на длине
волны 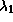 . При
. При 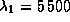
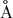 , как было показано в
задаче
, как было показано в
задаче  ,
, 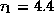 .
.
Обозначим искомую длину волны максимума в распределении энергии у
закатного Солнца через 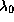 . Она определяется очевидным
условием
. Она определяется очевидным
условием
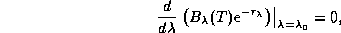
из которого все и следует. К сожалению, вычислений не избежать.
Воспользуемся этим случаем, чтобы поучиться делать их культурно.
Возьмем функцию Планка в приближении Вина
(в задаче  мы убедимся, что делать это можно):
мы убедимся, что делать это можно):
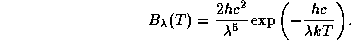
Тогда получаем следующее уравнение для нахождения 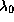 :
:
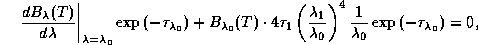
или
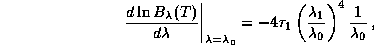
откуда в приближении Вина
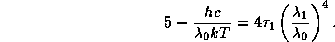
Но, с другой стороны, в приближении Вина длина волны
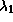 , на которой лежит максимум
, на которой лежит максимум 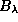 , так что
, так что

определяется условием

Поэтому, обозначив

мы можем переписать полученное выше уравнение, определяющее
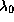 , в виде
, в виде
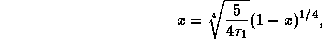
или, поскольку 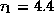 ,
,

Ясно, что x < 1, иначе Солнце у горизонта не было бы красным.
Однако без вычислений не обойтись.
Сначала получим грубую оценку корня,
линеаризовав уравнение с помощью разложения

справедливого при малых x. В этом приближении найдем, что x=0.62.
Какова точность этого приближения, пока неясно. Поскольку x не
очень мало, второй знак едва ли верен.
Уточнить значение корня можно итерациями, организованными по схеме
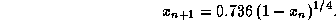
В качестве начального приближения возьмем 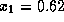 . Тогда получим
(калькулятор понадобится буквально на одну минуту!)
. Тогда получим
(калькулятор понадобится буквально на одну минуту!) 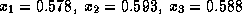 . Стоп. Ясно, что с точностью до двух значащих
цифр x=0.59, а потому 1/x=1.70. Вспоминая определение x, для
искомой длины волны максимума в распределении энергии в спектре
закатного Солнца находим
. Стоп. Ясно, что с точностью до двух значащих
цифр x=0.59, а потому 1/x=1.70. Вспоминая определение x, для
искомой длины волны максимума в распределении энергии в спектре
закатного Солнца находим
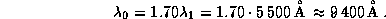
Последнее, что осталось сделать, -- показать применимость
приближения Вина. Поскольку
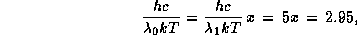
то 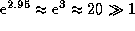 , и в области
, и в области
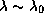 приближение Вина все еще применимо
(погрешность
приближение Вина все еще применимо
(погрешность 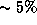 ).
).
©
В.В.Иванов,
А.В.Кривов,
П.А.Денисенков
HTML by Igor Drozdovsky
Последнее обновление:



Next: Звездные величины
Up: Задачи
Previous: Всемирное тяготение

 6.1
В подсолнечной точке темп притока энергии равен
6.1
В подсолнечной точке темп притока энергии равен 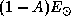 , где
, где
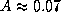 -- альбедо Луны,
-- альбедо Луны,
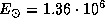 эрг/(см2c) -- солнечная постоянная.
Отток энергии происходит за счет излучения нагретого поверхностного
слоя почвы (в ИК-диапазоне), темп которого равен
эрг/(см2c) -- солнечная постоянная.
Отток энергии происходит за счет излучения нагретого поверхностного
слоя почвы (в ИК-диапазоне), темп которого равен
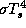 , где
, где 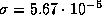 -- постоянная Стефана
(индекс s у
-- постоянная Стефана
(индекс s у 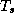 -- от surface, т.е. поверхность). Приравнивая
темпы нагрева и охлаждения, получаем
-- от surface, т.е. поверхность). Приравнивая
темпы нагрева и охлаждения, получаем

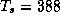 K, или 115o по Цельсию, так что босиком не
походишь -- обожжешь ступни. Эта оценка слегка завышена. Она была бы
строго верна, если бы Луна всегда была обращена одной стороной к
Солнцу (а не к Земле). Однако так как вращение Луны вокруг оси происходит
медленно, ошибка должна быть невелика.
K, или 115o по Цельсию, так что босиком не
походишь -- обожжешь ступни. Эта оценка слегка завышена. Она была бы
строго верна, если бы Луна всегда была обращена одной стороной к
Солнцу (а не к Земле). Однако так как вращение Луны вокруг оси происходит
медленно, ошибка должна быть невелика.



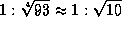 (см. формулу в решении задачи
(см. формулу в решении задачи 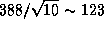 K, или
K, или 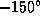 по
Цельсию -- жуткий мороз! (А железный лист в условии задачи зачем
понадобился, как вы думаете?)
по
Цельсию -- жуткий мороз! (А железный лист в условии задачи зачем
понадобился, как вы думаете?)
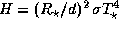 ,
где
,
где 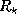 -- радиус звезды,
а d -- расстояние от нее до планеты.
Из этого потока доля 1-A,
поглощаемая поверхностью планеты, идет на ее нагрев.
Приравнивая скорости притока и оттока тепла в "подсолнечной" точке,
получаем
-- радиус звезды,
а d -- расстояние от нее до планеты.
Из этого потока доля 1-A,
поглощаемая поверхностью планеты, идет на ее нагрев.
Приравнивая скорости притока и оттока тепла в "подсолнечной" точке,
получаем
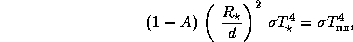
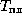 в "подсолнечной" точке находим
в "подсолнечной" точке находим
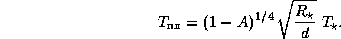

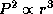 , могли бы написать это сразу.
, могли бы написать это сразу.

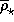 .
.
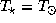 и
и 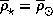 ,
а P взять равным 1 году.
Приравнивая температуры на планете и на Луне, для периода обращения
планеты в годах получаем следующее простое выражение:
,
а P взять равным 1 году.
Приравнивая температуры на планете и на Луне, для периода обращения
планеты в годах получаем следующее простое выражение:
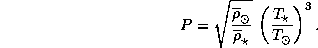
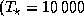 K,
K,
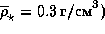 период
составляет около 10 лет.
период
составляет около 10 лет.
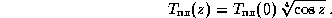
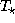 и
и 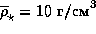 ,
,
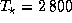 K), то
чтобы на ней можно было сносно жить -- не
замерзнуть и не изжариться -- продолжительность года
должна была бы составлять всего
K), то
чтобы на ней можно было сносно жить -- не
замерзнуть и не изжариться -- продолжительность года
должна была бы составлять всего 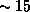 земных суток.
Впадать в долгую зимнюю спячку медведям не удалось бы!
земных суток.
Впадать в долгую зимнюю спячку медведям не удалось бы!
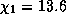 эВ.
Поэтому число атомов водорода
эВ.
Поэтому число атомов водорода 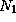 , которое может быть ионизовано
за счет кинетической энергии движения Земли, равно
, которое может быть ионизовано
за счет кинетической энергии движения Земли, равно

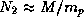 ,
где
,
где 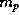 -- масса протона. Подставляя известные числовые
значения физических величин, находим отношение
-- масса протона. Подставляя известные числовые
значения физических величин, находим отношение

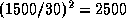 раз меньше, или около
4эВ, что составляет 0.3 от энергии связи атома водорода (13.6эВ).
Отсюда непосредственно следует, в согласии с полученным выше, что
кинетической энергии движения Земли хватит на ионизацию массы
водорода, составляющей 0.3 ее собственной массы.
раз меньше, или около
4эВ, что составляет 0.3 от энергии связи атома водорода (13.6эВ).
Отсюда непосредственно следует, в согласии с полученным выше, что
кинетической энергии движения Земли хватит на ионизацию массы
водорода, составляющей 0.3 ее собственной массы.
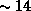 км/с.
км/с.
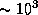 г/см2.
Поэтому масса столба воздуха сечением 1 см2
равна
г/см2.
Поэтому масса столба воздуха сечением 1 см2
равна 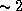 м.
Далее, из формулы
м.
Далее, из формулы


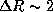 м будет
м будет 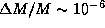 .
.
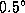 .
А описанная картина объясняется так же, как и кажущаяся сходимость
параллельных рельсов или расходимость траекторий метеоров
из радианта -- явлением перспективы.
.
А описанная картина объясняется так же, как и кажущаяся сходимость
параллельных рельсов или расходимость траекторий метеоров
из радианта -- явлением перспективы.
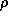 убывает с высотой по закону (так называемая
барометрическая формула; кстати, как вы думаете, почему она так называется?)
убывает с высотой по закону (так называемая
барометрическая формула; кстати, как вы думаете, почему она так называется?)

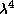 . Для синих
лучей она окажется больше единицы, и это излучение будет сильно ослаблено.
Восход и закат Солнца едва ли будут видны -- при приближении к
горизонту диск Солнца будет постепенно становиться все менее ярким, и
еще до достижения горизонта он скорее всего перестанет быть виден.
Ночью звезд на небе будет совсем мало, и они будут красновато-желтыми.
Вблизи горизонта, на зенитных расстояниях
. Для синих
лучей она окажется больше единицы, и это излучение будет сильно ослаблено.
Восход и закат Солнца едва ли будут видны -- при приближении к
горизонту диск Солнца будет постепенно становиться все менее ярким, и
еще до достижения горизонта он скорее всего перестанет быть виден.
Ночью звезд на небе будет совсем мало, и они будут красновато-желтыми.
Вблизи горизонта, на зенитных расстояниях 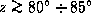 ,
их вовсе не будет видно, так как оптическая толщина по лучу зрения
,
их вовсе не будет видно, так как оптическая толщина по лучу зрения
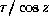 будет
будет 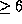 .
.
 порядка единицы. Действительно, если
порядка единицы. Действительно, если 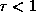 , то
чем меньше
, то
чем меньше 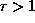 с ростом
с ростом 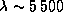
 (максимум чувствительности
глаза) различие будет по меньшей мере 20-кратным.
(максимум чувствительности
глаза) различие будет по меньшей мере 20-кратным.

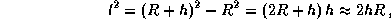
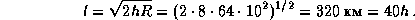
 ,
который солнечные лучи проходят в атмосфере при наблюдении восхода
с горы высотой
,
который солнечные лучи проходят в атмосфере при наблюдении восхода
с горы высотой 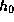 , составляет
, составляет

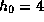 км мы имеем
км мы имеем 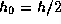 , так что
, так что

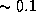 (в действительности даже несколько больше, см. ниже).
По касательной, как мы только что убедились, она должна
быть в 40 раз больше, т.е.
(в действительности даже несколько больше, см. ниже).
По касательной, как мы только что убедились, она должна
быть в 40 раз больше, т.е. 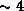 .
Поэтому в момент восхода солнечное излучение на
.
Поэтому в момент восхода солнечное излучение на
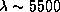
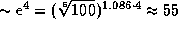 раз
(или на
раз
(или на 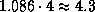 звездных величины).
На пути от A до B луч ослабляется дополнительно в
звездных величины).
На пути от A до B луч ослабляется дополнительно в
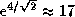 раз, так что диск Солнца
при наблюдении восхода с высокой горы оказывается гораздо менее
ярким, чем с корабля.
раз, так что диск Солнца
при наблюдении восхода с высокой горы оказывается гораздо менее
ярким, чем с корабля.
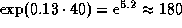 раз.
При наблюдении с горы высотой
раз.
При наблюдении с горы высотой 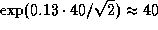 раз.
Как видим, полученные выше оценки, относящиеся к чисто газовой атмосфере,
вполне могут давать яркость Солнца в момент восхода с ошибкой
в несколько раз.
раз.
Как видим, полученные выше оценки, относящиеся к чисто газовой атмосфере,
вполне могут давать яркость Солнца в момент восхода с ошибкой
в несколько раз.
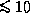 % в горизонтальной оптической толщине).
Можно считать, что плотность в атмосфере меняется с высотой h по
барометрическому закону
% в горизонтальной оптической толщине).
Можно считать, что плотность в атмосфере меняется с высотой h по
барометрическому закону

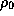 -- плотность воздуха на уровне моря.
Рассмотрим сначала случай наблюдения из точки A, т.е. с уровня моря.
Тогда воздушная масса на горизонтальном луче оказывается равной
-- плотность воздуха на уровне моря.
Рассмотрим сначала случай наблюдения из точки A, т.е. с уровня моря.
Тогда воздушная масса на горизонтальном луче оказывается равной
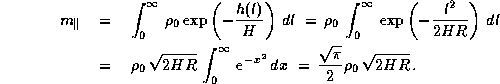
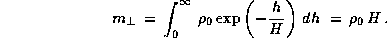

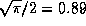 .
Его отличие от единицы нужно было бы учитывать, если бы
оптическая толщина атмосферы по нормали была бы известна с точностью
.
Его отличие от единицы нужно было бы учитывать, если бы
оптическая толщина атмосферы по нормали была бы известна с точностью
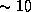 %, чего из-за переменной запыленности воздуха на самом деле нет.
%, чего из-за переменной запыленности воздуха на самом деле нет.


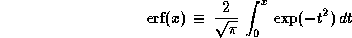
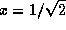 .
Разлагая экспоненту в ряд и интегрируя затем этот ряд почленно,
находим, что
.
Разлагая экспоненту в ряд и интегрируя затем этот ряд почленно,
находим, что
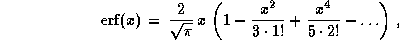
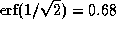 .
Это очень близко к числу
.
Это очень близко к числу 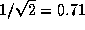 , полученному нами ранее для
отношения воздушных масс на пути AB и на луче AS в предположении,
что атмосфера однородна.
, полученному нами ранее для
отношения воздушных масс на пути AB и на луче AS в предположении,
что атмосфера однородна.
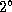 (покажите это, вычислив угол
(покажите это, вычислив угол 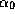 ),
однако это приводит к тому, что солнечные лучи проходят
дополнительный путь
),
однако это приводит к тому, что солнечные лучи проходят
дополнительный путь 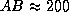 км, что увеличивает
массу и оптическую толщину столба воздуха на их пути
почти на 70% и делает Солнце значительно менее ярким
(экспонента -- это не линейная функция!).
Но когда восходящее Солнце достигнет математического горизонта,
оно будет уже в
км, что увеличивает
массу и оптическую толщину столба воздуха на их пути
почти на 70% и делает Солнце значительно менее ярким
(экспонента -- это не линейная функция!).
Но когда восходящее Солнце достигнет математического горизонта,
оно будет уже в 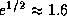 раза более
ярким, чем в случае его наблюдения на горизонте с уровня моря.
Убедитесь в этом самостоятельно.
раза более
ярким, чем в случае его наблюдения на горизонте с уровня моря.
Убедитесь в этом самостоятельно.
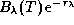 , где
, где
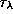 -- оптическая толщина атмосферы вдоль горизонтального
луча. При молекулярном рассеянии
-- оптическая толщина атмосферы вдоль горизонтального
луча. При молекулярном рассеянии 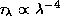 (закон Рэлея). Положим
(закон Рэлея). Положим

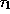 -- горизонтальная оптическая толщина атмосферы на длине
волны
-- горизонтальная оптическая толщина атмосферы на длине
волны 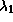 . При
. При 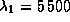
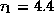 .
.
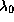 . Она определяется очевидным
условием
. Она определяется очевидным
условием
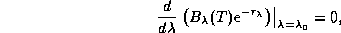
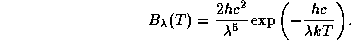
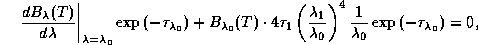
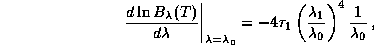
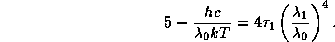
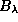 , так что
, так что



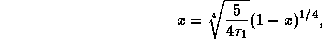


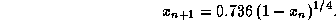
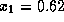 . Тогда получим
(калькулятор понадобится буквально на одну минуту!)
. Тогда получим
(калькулятор понадобится буквально на одну минуту!) 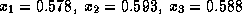 . Стоп. Ясно, что с точностью до двух значащих
цифр x=0.59, а потому 1/x=1.70. Вспоминая определение x, для
искомой длины волны максимума в распределении энергии в спектре
закатного Солнца находим
. Стоп. Ясно, что с точностью до двух значащих
цифр x=0.59, а потому 1/x=1.70. Вспоминая определение x, для
искомой длины волны максимума в распределении энергии в спектре
закатного Солнца находим
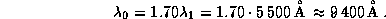
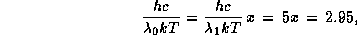
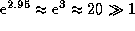 , и в области
, и в области
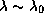 приближение Вина все еще применимо
(погрешность
приближение Вина все еще применимо
(погрешность 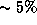 ).
).