


Next: Физика звезд
Up: Задачи
Previous: Солнце
Решения
 11.1
Из соотношения масса -- cветимость
11.1
Из соотношения масса -- cветимость 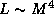 для
для 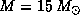 находим
находим
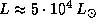 .
Эффективная температура звезды главной последовательности спектрального
класса B0 равна
.
Эффективная температура звезды главной последовательности спектрального
класса B0 равна
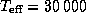 K.
Радиус звезды найдем из
соотношения между светимостью, радиусом и эффективной температурой
K.
Радиус звезды найдем из
соотношения между светимостью, радиусом и эффективной температурой

что дает
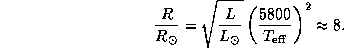
Поэтому
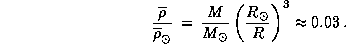
Средняя плотность Солнца 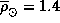 г/см3,
так что
г/см3,
так что 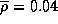 г/см3.
Не правда ли, полученный результат противоречит тому,
что подсказывает "здравый смысл" --
будто бы с ростом массы плотность должна расти.
Так называемый "здравый смысл" имеет разумную область применимости --
свою у каждого, и подобные задачи помогут вам расширить ее.
г/см3.
Не правда ли, полученный результат противоречит тому,
что подсказывает "здравый смысл" --
будто бы с ростом массы плотность должна расти.
Так называемый "здравый смысл" имеет разумную область применимости --
свою у каждого, и подобные задачи помогут вам расширить ее.
 11.2
Деля светимость Солнца на площадь его поверхности, получаем поток с
1 см2:
11.2
Деля светимость Солнца на площадь его поверхности, получаем поток с
1 см2:
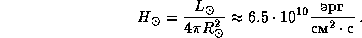
По определению, поток с единицы поверхности Солнца
связан с его эффективной температурой следующим образом:

где 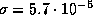 -- постоянная Стефана. Подставляя
сюда найденное выше значение потока, получим
для Солнца
-- постоянная Стефана. Подставляя
сюда найденное выше значение потока, получим
для Солнца

Поучительно перевести это число в нечто более ощутимое "для
обывателя".
Поток с поверхности Солнца соответствует тому,
что с 1 см2 излучается 6.5 кВт (проверьте!).
 11.3
Мы имеем
11.3
Мы имеем

Найдем дифференциал логарифма L:
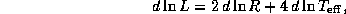
или
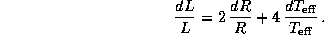
Для малых приращений радиуса и температуры последнее точное выражение можно
заменить на приближенное
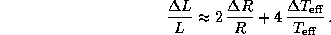
Подставляя сюда из условия задачи
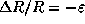 и
и
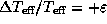 ,
приближенно имеем
,
приближенно имеем
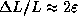 , так что
при
, так что
при 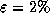 светимость звезды возрастет примерно на 4%.
светимость звезды возрастет примерно на 4%.
 11.4
При сравнении абсолютных звездных величин считается, что звезды находятся
на одном и том же стандартном расстоянии (10 пк). В этом
случае освещенности от разных звезд просто пропорциональны их светимостям.
Тогда для нашей пары звезд имеем
11.4
При сравнении абсолютных звездных величин считается, что звезды находятся
на одном и том же стандартном расстоянии (10 пк). В этом
случае освещенности от разных звезд просто пропорциональны их светимостям.
Тогда для нашей пары звезд имеем
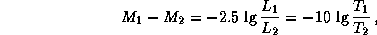
где мы воспользовались известным соотношением между светимостью, радиусом и
эффективной температурой звезды (см. предыдущую задачу) и учли, что
по условию 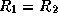 . Пусть первая звезда горячее (на 10%) второй,
т.е.
. Пусть первая звезда горячее (на 10%) второй,
т.е. 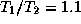 . Учитывая малое отличие отношения температур от
единицы, приближенно находим
. Учитывая малое отличие отношения температур от
единицы, приближенно находим
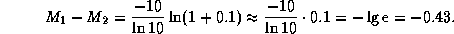
Тот факт, что 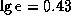 , следует помнить.
, следует помнить.
 11.5
Дифференцируя формулу, выражающую закон Стефана-Больцмана,
легко получить, считая радиус постоянным
(см., например, задачу
11.5
Дифференцируя формулу, выражающую закон Стефана-Больцмана,
легко получить, считая радиус постоянным
(см., например, задачу  )
)

Таким образом, чтобы светимости двух звезд одинакового радиуса
отличались на 4%, их температуры должны разниться на 1%.
Далее, по закону смещения Вина 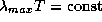 ,
и поэтому
,
и поэтому 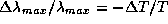 ,
так что при увеличении температуры на 1% длина волны максимума в
распределении энергии уменьшается тоже на 1%. Сходным образом
показывается, что интенсивность в максимуме при росте температуры на
1% увеличивается на 5%, а интенсивность в рэлей-джинсовской
области -- на 1% (поймите, почему).
,
так что при увеличении температуры на 1% длина волны максимума в
распределении энергии уменьшается тоже на 1%. Сходным образом
показывается, что интенсивность в максимуме при росте температуры на
1% увеличивается на 5%, а интенсивность в рэлей-джинсовской
области -- на 1% (поймите, почему).
 11.6
Высота однородной атмосферы связана с температурой T, ускорением силы
тяжести g и средней молярной массой
11.6
Высота однородной атмосферы связана с температурой T, ускорением силы
тяжести g и средней молярной массой 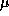 следующим соотношением:
следующим соотношением:

где 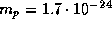 г --
атомная единица массы.
Для Солнца
г --
атомная единица массы.
Для Солнца 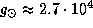 см/с2,
см/с2, 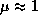 (атмосфера Солнца состоит в основном из водорода и он не ионизован),
наконец,
(атмосфера Солнца состоит в основном из водорода и он не ионизован),
наконец, 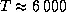 K,
что в итоге дает
K,
что в итоге дает 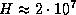 см, или около 200 км.
см, или около 200 км.
Ускорение силы тяжести на поверхности белого карлика можно выразить через
его массу и радиус в солнечных единицах:
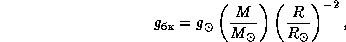
откуда находим для нашего белого карлика 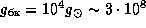 см/с2. (Это колоссальное
ускорение. Материальная точка, движущаяся с таким ускорением, за
первую секунду проходит путь в 1500 км, что составляет около
четверти радиуса белого карлика.) Учитывая также, что при
см/с2. (Это колоссальное
ускорение. Материальная точка, движущаяся с таким ускорением, за
первую секунду проходит путь в 1500 км, что составляет около
четверти радиуса белого карлика.) Учитывая также, что при
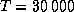 K водород ионизован, так что
K водород ионизован, так что 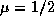 , для высоты
однородной атмосферы белого карлика получаем
, для высоты
однородной атмосферы белого карлика получаем
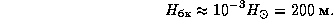
Уместно вспомнить, что для Земли, имеющей тот же приблизительно
радиус, что и у белого карлика, высота однородной атмосферы
составляет 8 км.
 11.7
Мы имеем
11.7
Мы имеем

где  -- постоянная Стефана.
Если светимость и радиус выразить в солнечных единицах, то получим отсюда
-- постоянная Стефана.
Если светимость и радиус выразить в солнечных единицах, то получим отсюда
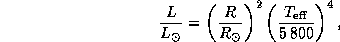
где использовано значение эффективной температуры Солнца
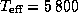 K.
С помощью последней формулы находим,
что светимость белого карлика в светимостях Солнца равна
K.
С помощью последней формулы находим,
что светимость белого карлика в светимостях Солнца равна

Множителю 16 отвечает разница почти точно в 3 звездные величины
(это полезно помнить; вот более точное значение: 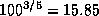 ).
Поэтому абсолютная болометрическая звездная величина белого карлика
будет на 3 звездные величины больше, чем у Солнца. Так чему же она равна?
).
Поэтому абсолютная болометрическая звездная величина белого карлика
будет на 3 звездные величины больше, чем у Солнца. Так чему же она равна?
 11.8
Из сравнения абсолютных звездных величин белого карлика и Солнца найдем
отношение их светимостей:
11.8
Из сравнения абсолютных звездных величин белого карлика и Солнца найдем
отношение их светимостей:
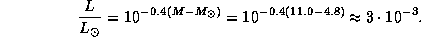
Далее, по формуле из решения предыдущей задачи оценим радиус белого карлика
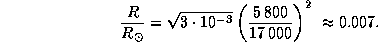
Это около 5000 км, т.е. меньше радиуса Земли (6400 км).
 11.9
Фотон с энергией
11.9
Фотон с энергией 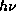 несет импульс
несет импульс 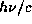 в направлении своего
полета. После отражения от неподвижной или медленно удаляющейся от
звезды фольги импульс фотона оказывается направлен в
противоположную сторону,
а его величина та же, что и до отражения. Поэтому при отражении
каждого фотона фольге передается импульс
в направлении своего
полета. После отражения от неподвижной или медленно удаляющейся от
звезды фольги импульс фотона оказывается направлен в
противоположную сторону,
а его величина та же, что и до отражения. Поэтому при отражении
каждого фотона фольге передается импульс 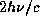 . Скорость передачи
импульса есть сила светового давления на фольгу.
В расчете на единицу площади она равна,
таким образом,
. Скорость передачи
импульса есть сила светового давления на фольгу.
В расчете на единицу площади она равна,
таким образом, 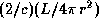 , где L -- светимость и
r -- расстояние до звезды.
Чтобы фольга с сидящим на ней комаром пренебрежимо малой массы
улетела к другим звездам, световое давление должно превышать силу
притяжения. В расчете на единицу площади поверхности фольги толщины
H, изготовленной из материала с плотностью
, где L -- светимость и
r -- расстояние до звезды.
Чтобы фольга с сидящим на ней комаром пренебрежимо малой массы
улетела к другим звездам, световое давление должно превышать силу
притяжения. В расчете на единицу площади поверхности фольги толщины
H, изготовленной из материала с плотностью 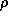 , сила притяжения
составляет
, сила притяжения
составляет 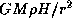 , где M -- масса звезды.
Итак, чтобы фольга могла служить фотонным
парусом, на котором можно улететь от звезды на бесконечность, должно
выполняться условие
, где M -- масса звезды.
Итак, чтобы фольга могла служить фотонным
парусом, на котором можно улететь от звезды на бесконечность, должно
выполняться условие

откуда

Здесь мы неявно предполагаем, что первоначально фольга покоится
(а не движется вокруг звезды, скажем, по круговой орбите).
Обратите внимание, что r выпало. Причина, конечно, в том, что и
сила притяжения, и поток зависят от r одинаково (как 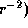 , так
что если давление излучения превышает силу тяжести на каком-то
расстоянии r, то оно превышает ее везде. Фольга металлическая, так
что можно принять
, так
что если давление излучения превышает силу тяжести на каком-то
расстоянии r, то оно превышает ее везде. Фольга металлическая, так
что можно принять 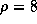 г/см3 (как у железа). Далее, для звезды
класса O5V имеем
г/см3 (как у железа). Далее, для звезды
класса O5V имеем 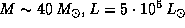 .
Подставляя численные значения, находим, что H < 0.25 см. Как видим, в
качестве "фольги" вполне сошел бы и покрашенный в белую краску лист
кровельного железа!
.
Подставляя численные значения, находим, что H < 0.25 см. Как видим, в
качестве "фольги" вполне сошел бы и покрашенный в белую краску лист
кровельного железа!
Возлежа вместо дивана на большом железном листе,
от звезды класса O5 мог бы отправиться в межзвездное
странствие не только комар, но и Обломов.
А теперь, пользуясь полученной формулой, немного пофантазируйте сами
о межзвездных перелетах на фотонных парусах -- об их
продолжительности, например. Что можно сказать о
фотонных парусах для нашей Солнечной системы? Они даже были
изготовлены, но из-за ограниченности финансирования космических
программ до их реального использования дело пока не дошло.
Какова должна быть площадь невесомого фотонного паруса,
на котором от Солнца к звездам могла бы улететь муха массой 1 г?
©
В.В.Иванов,
А.В.Кривов,
П.А.Денисенков
HTML by Igor Drozdovsky
Последнее обновление:



Next: Физика звезд
Up: Задачи
Previous: Солнце

 11.1
Из соотношения масса -- cветимость
11.1
Из соотношения масса -- cветимость 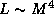 для
для 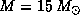 находим
находим
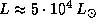 .
Эффективная температура звезды главной последовательности спектрального
класса B0 равна
.
Эффективная температура звезды главной последовательности спектрального
класса B0 равна
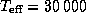 K.
Радиус звезды найдем из
соотношения между светимостью, радиусом и эффективной температурой
K.
Радиус звезды найдем из
соотношения между светимостью, радиусом и эффективной температурой

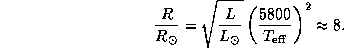
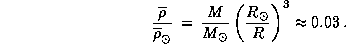
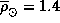 г/см3,
так что
г/см3,
так что 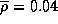 г/см3.
Не правда ли, полученный результат противоречит тому,
что подсказывает "здравый смысл" --
будто бы с ростом массы плотность должна расти.
Так называемый "здравый смысл" имеет разумную область применимости --
свою у каждого, и подобные задачи помогут вам расширить ее.
г/см3.
Не правда ли, полученный результат противоречит тому,
что подсказывает "здравый смысл" --
будто бы с ростом массы плотность должна расти.
Так называемый "здравый смысл" имеет разумную область применимости --
свою у каждого, и подобные задачи помогут вам расширить ее.



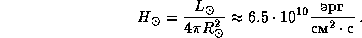

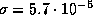 -- постоянная Стефана. Подставляя
сюда найденное выше значение потока, получим
для Солнца
-- постоянная Стефана. Подставляя
сюда найденное выше значение потока, получим
для Солнца


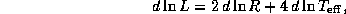
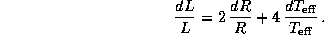
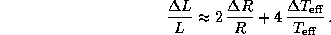
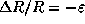 и
и
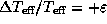 ,
приближенно имеем
,
приближенно имеем
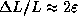 , так что
при
, так что
при 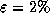 светимость звезды возрастет примерно на 4%.
светимость звезды возрастет примерно на 4%.
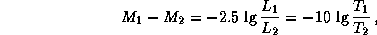
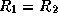 . Пусть первая звезда горячее (на 10%) второй,
т.е.
. Пусть первая звезда горячее (на 10%) второй,
т.е. 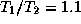 . Учитывая малое отличие отношения температур от
единицы, приближенно находим
. Учитывая малое отличие отношения температур от
единицы, приближенно находим
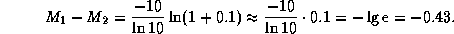
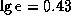 , следует помнить.
, следует помнить.

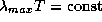 ,
и поэтому
,
и поэтому 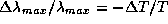 ,
так что при увеличении температуры на 1% длина волны максимума в
распределении энергии уменьшается тоже на 1%. Сходным образом
показывается, что интенсивность в максимуме при росте температуры на
1% увеличивается на 5%, а интенсивность в рэлей-джинсовской
области -- на 1% (поймите, почему).
,
так что при увеличении температуры на 1% длина волны максимума в
распределении энергии уменьшается тоже на 1%. Сходным образом
показывается, что интенсивность в максимуме при росте температуры на
1% увеличивается на 5%, а интенсивность в рэлей-джинсовской
области -- на 1% (поймите, почему).
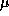 следующим соотношением:
следующим соотношением:

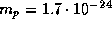 г --
атомная единица массы.
Для Солнца
г --
атомная единица массы.
Для Солнца 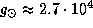 см/с2,
см/с2, 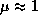 (атмосфера Солнца состоит в основном из водорода и он не ионизован),
наконец,
(атмосфера Солнца состоит в основном из водорода и он не ионизован),
наконец, 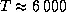 K,
что в итоге дает
K,
что в итоге дает 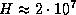 см, или около 200 км.
см, или около 200 км.
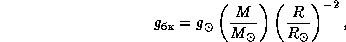
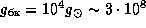 см/с2. (Это колоссальное
ускорение. Материальная точка, движущаяся с таким ускорением, за
первую секунду проходит путь в 1500 км, что составляет около
четверти радиуса белого карлика.) Учитывая также, что при
см/с2. (Это колоссальное
ускорение. Материальная точка, движущаяся с таким ускорением, за
первую секунду проходит путь в 1500 км, что составляет около
четверти радиуса белого карлика.) Учитывая также, что при
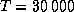 K водород ионизован, так что
K водород ионизован, так что 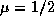 , для высоты
однородной атмосферы белого карлика получаем
, для высоты
однородной атмосферы белого карлика получаем
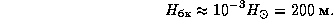

 -- постоянная Стефана.
Если светимость и радиус выразить в солнечных единицах, то получим отсюда
-- постоянная Стефана.
Если светимость и радиус выразить в солнечных единицах, то получим отсюда
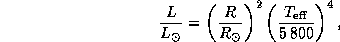
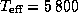 K.
С помощью последней формулы находим,
что светимость белого карлика в светимостях Солнца равна
K.
С помощью последней формулы находим,
что светимость белого карлика в светимостях Солнца равна

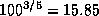 ).
Поэтому абсолютная болометрическая звездная величина белого карлика
будет на 3 звездные величины больше, чем у Солнца. Так чему же она равна?
).
Поэтому абсолютная болометрическая звездная величина белого карлика
будет на 3 звездные величины больше, чем у Солнца. Так чему же она равна?
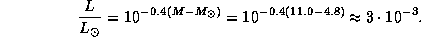
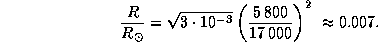
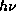 несет импульс
несет импульс 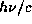 в направлении своего
полета. После отражения от неподвижной или медленно удаляющейся от
звезды фольги импульс фотона оказывается направлен в
противоположную сторону,
а его величина та же, что и до отражения. Поэтому при отражении
каждого фотона фольге передается импульс
в направлении своего
полета. После отражения от неподвижной или медленно удаляющейся от
звезды фольги импульс фотона оказывается направлен в
противоположную сторону,
а его величина та же, что и до отражения. Поэтому при отражении
каждого фотона фольге передается импульс 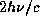 . Скорость передачи
импульса есть сила светового давления на фольгу.
В расчете на единицу площади она равна,
таким образом,
. Скорость передачи
импульса есть сила светового давления на фольгу.
В расчете на единицу площади она равна,
таким образом, 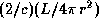 , где L -- светимость и
r -- расстояние до звезды.
Чтобы фольга с сидящим на ней комаром пренебрежимо малой массы
улетела к другим звездам, световое давление должно превышать силу
притяжения. В расчете на единицу площади поверхности фольги толщины
H, изготовленной из материала с плотностью
, где L -- светимость и
r -- расстояние до звезды.
Чтобы фольга с сидящим на ней комаром пренебрежимо малой массы
улетела к другим звездам, световое давление должно превышать силу
притяжения. В расчете на единицу площади поверхности фольги толщины
H, изготовленной из материала с плотностью 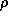 , сила притяжения
составляет
, сила притяжения
составляет 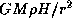 , где M -- масса звезды.
Итак, чтобы фольга могла служить фотонным
парусом, на котором можно улететь от звезды на бесконечность, должно
выполняться условие
, где M -- масса звезды.
Итак, чтобы фольга могла служить фотонным
парусом, на котором можно улететь от звезды на бесконечность, должно
выполняться условие


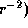 , так
что если давление излучения превышает силу тяжести на каком-то
расстоянии r, то оно превышает ее везде. Фольга металлическая, так
что можно принять
, так
что если давление излучения превышает силу тяжести на каком-то
расстоянии r, то оно превышает ее везде. Фольга металлическая, так
что можно принять 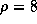 г/см3 (как у железа). Далее, для звезды
класса O5V имеем
г/см3 (как у железа). Далее, для звезды
класса O5V имеем 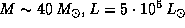 .
Подставляя численные значения, находим, что H < 0.25 см. Как видим, в
качестве "фольги" вполне сошел бы и покрашенный в белую краску лист
кровельного железа!
.
Подставляя численные значения, находим, что H < 0.25 см. Как видим, в
качестве "фольги" вполне сошел бы и покрашенный в белую краску лист
кровельного железа!